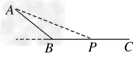
1、选择题  如图所示，斜面AB和水平面BC是由同一板材上截下的两段，在B处用小圆弧连接．将小铁块(可视为质点)从A处由静止释放后，它沿斜面向下滑行，进入平面，最终静止于P处．若从该板材上再截下一段，搁置在A、P之间，构成一个新的斜面，再将小铁块放回A处，并轻推一下使之具有初速度v0，沿新斜面向下滑动．关于此情况下小铁块的运动情况的描述正确的是

[? ]
A．小铁块不能到达P点
B．小铁块的初速度必须足够大才能到达P点
C．小铁块能否到达P点与小铁块的质量无关
D．以上说法均不对

参考答案：C

本题解析：

本题难度：一般

2、计算题  （20分）如图所示，A、B两个小物体（可看成质点）的质量分别为2m、m，它们栓接在跨过定滑轮的细绳两端，细绳不可伸长，且能承受足够大的拉力。B物体悬吊着静止时，A也静止在地面上，A、B与定滑轮轮轴之间的竖直距离分别为2l、l。现将B物体竖直向上提高距离l，再将其从静止释放。每次细绳被拉直时A、B速度的大小立即变成相等，且速度方向相反，由于细绳被拉直的时间极短，此过程中重力的作用可以忽略不计。物体与地面接触时，速度立即变为0，直到再次被细绳拉起。细绳始终在滑轮上，且不计一切摩擦。重力加速度为g。求
（1）细绳第一次被拉直瞬间绳对A冲量的大小；
（2）A第一次上升过程距离地面的最大高度；
（3）A运动的总路程。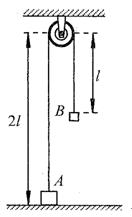

参考答案：（1）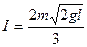
（2）
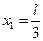
（3）

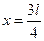
本题解析：
（1）B做自由落体，下降高度为I时的速度为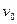
根据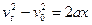得
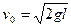?（3分）
此时细绳被拉直，A、B速度的大小立即变成，
设绳子对A、B的冲量大小为I，根据动量定理得
对B??（1分）
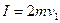对A??（1分）
解得细绳第一次被拉直瞬间绳对A冲量的大小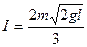?（2分）
（2）由（1）可得A第一次离开地面时速度的大小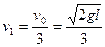（2分）
从A离开地面到A再次回到地面的过程中，A、B组成的系统机械能守恒，
假设A第一次上升过程距离地面的最大高度为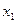，则
?（2分）
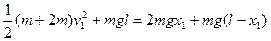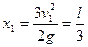解得?（2分）
（3）从A离开地面到A再次回到地面的过程中，A、B组成的系统机械能守恒，
所以，A再次回到地面时速度的大小依然为，
即B再次回到距离地面高度为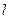时速度的大小也为。
此后B做竖直上抛运动，落回距离地面高度为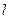时速度的大小还是。（1分）
根据（1）求解可得A第二次离开地面时速度的大小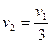（1分）
同理可求A第二次离开地面上升的最大高度为
（1分）
……
A第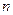次离开地面时速度的大小?（1分）
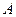同理可求第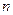次离开地面上升的最大高度为
?（1分）
由于A的质量大于B的质量，A最终会静止在地面上。
所以A运动的总路程

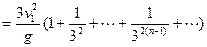
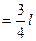
本题难度：一般

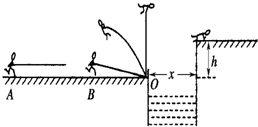
3、简答题  如图所示，一位质量m=60kg、参加“挑战极限运动”的业余选手，要越过一宽为x=2.5m的水沟后跃上高为h=2.0m的平台．他采用的方法是：手握一根长L=3.25m的轻质弹性杆一端，从A点由静止开始匀加速助跑，至B点时杆另一端抵在O点的阻挡物上，接着杆发生形变，同时人蹬地后被弹起，到达最高点时杆处于竖直状态，人的重心在杆的顶端，此刻人放开杆水平飞出并趴落到平台上，运动过程中空气阻力可忽略不计．
（1）设人到达B点时速度vB=8m/s，人匀加速运动的加速度a=2m/s2，求助跑距离xAB；
（2）人要最终到达平台，在最高点飞出时刻的速度应至少多大？（g=10m/s2）
（3）设人跑动过程中重心离地高度H=0.8m，在（1）、（2）两问的条件下，在B点人蹬地弹起瞬间应至少再做多少功？

参考答案：（1）由运动学公式 v2B=2axm
可得xAB=v2B2a=16m
即助跑距离xAB为16m．
（2）设人在最高点最小速度为v
人做平抛运动过程，有
L-h=12gt2
x=vt
解得 v=x?

本题解析：

本题难度：一般

4、选择题  如图1所示，质量为m的物体静止于倾角为α的斜面体上，现对斜面体施
加一水平向左的推力F，使物体随斜面体一起沿水平面向左匀速移动x，
则在此匀速运动过程中斜面体对物体所做的功为? (　　)

A．Fx
B．mgxcosαsinα
C．mgxsinα
D．0

参考答案：D

本题解析：由于物体做匀速运动，其处于平衡状态．物体动能和势能在运动过程中都不发生变化，故根据动能定理知合外力对物体做功为零．而重力做功为零，所以斜面体对物体做功为零，故应选D.

本题难度：简单

5、选择题  如图甲所示，一轻弹簧的两端与质量分别是m1和m2的两木块A、B相连，静止在光滑水平面上．现使A瞬间获得水平向右的速度v=3m/s，以此时刻为计时起点，两木块的速度随时间变化规律如图乙所示，从图示信息可知（　　）
A．t1时刻弹簧最短，t3时刻弹簧最长
B．从t1时刻到t2时刻弹簧由伸长状态恢复到原长
C．两木块的质量之比为m1：m2=1：2
D．在t2时刻两木块动能之比为EK1：EK2=1：4