1、简答题  请估算地月之间的距离。（保留一位有效数字）

参考答案：4×105(Km)

本题解析：月球是绕地球转的，由开普勒第三定律可知，所有绕地球转动的天体都满足
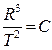，为了解决地月距离，就需要寻找一个熟悉的，便于计算的绕地球转动
的天体——同步卫星，同步卫星的周期T1=1天。轨道半径R1=6R0+R0=7R0，而月球周期T2=27天。
解答：?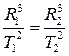

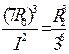
∴R2=7R0×32=63R0=4×105(Km)

本题难度：一般

2、选择题  极地卫星的运行轨道平面通过地球的南北两极（轨道可视为圆轨道）。如图所示，若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方，所用时间为t，已知地球半径为R（地球可看做球体），地球表面的重力加速度为g，引力常量为G，由以上条件可知?

A．地球的质量为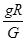
B．卫星运行的角速度为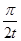
C．卫星运行的线速度为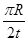
D．卫星距地面的高度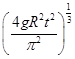

参考答案：B

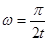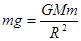本题解析：极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方，绕过的角度为900，所用时间为t，角速度为；根据，解得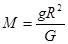；卫星运行的线速度为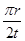（r为卫星的轨道半径）；，解得r=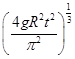,卫星距地面高度为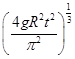-R。选项B正确。

本题难度：一般

3、简答题  某星球上，宇航员用弹簧秤称得质量为m的物体重量为F，乘宇宙飞船在靠近该星球表面空间飞行，测得环绕周期为T，引力常量为G，试求该星球的质量．

参考答案：m物体在星球表面的重量等于万有引力，设星球半径为R，星球质量为M
则：F=GMmR2，
飞船绕该星球飞行时，万有引力提供向心力：GMmR2=m4π2T2R，
得：M=T4F316π4Gm3?
答：求该星球的质量M=T4F316π4Gm3

本题解析：

本题难度：一般

4、填空题  一个物体的质量为m，在地球表面受到的重力为mg，将它带到距地面的高度为地球半径的2倍处，它的重力为______．

参考答案：设：地球的质量为M，半径为R，设万有引力常量为G，根据万有引力等于重力，
则有：GMmR2=mg…①
在距地面高度为地球半径的2倍时：GMm(3R)2=F…②
由①②联立得：
F=mg9
故答案为：mg9

本题解析：

本题难度：一般

5、选择题  一飞船绕地球做匀速园周运动，飞船离地面的高度为h，其内有一质量为m的人站在可称体重的台秤上，用R表示地球半径，g表示地球表面的重力加速度，g，表示飞船所在处的地球引力加速度，FN表示人对台秤的压力，则下列判断正确的是（　　）
A．g，=0
B．g，=

参考答案：A、忽略地球自转的影响，根据万有引力等于重力列出等式
在地球表面：GMmR2=mg
在离地面的高度为h处：GMm(R+h)2=mg，
解得：g=R2(R+h)2g，故A错误，B正确．
C、在绕地球做匀速园周运动的飞船内，各个物体处于完全失重的状态．
各个物体的重力完全提供向心力．
所以人站在可称体重的台秤上，人与台秤无弹力，所以FN=0，故C正确，D错误．
故选BC．

本题解析：

本题难度：一般