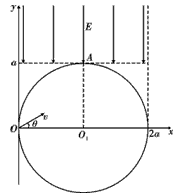
1、计算题  如图所示，在坐标系xOy内有一半径为a的圆形区域，圆心坐标为O1（a，0），圆内分布有垂直纸面向里的匀强磁场。在直线y＝a的上方和直线x＝2a的左侧区域内，有一沿y轴负方向的匀强电场，场强大小为E。一质量为m、电荷量为+q（q>0）的粒子以速度v从O点垂直于磁场方向射入，当速度方向沿x轴正方向时，粒子恰好从O1点正上方的A点射出磁场，不计粒子重力。
（1）求磁感应强度B的大小；
（2）粒子在第一象限内运动到最高点时的位置坐标；
（3）若粒子以速度v从O点垂直于磁场方向射入第一象限，当速度方向沿x轴正方向的夹角θ=30°时，求粒子从射入磁场到最终离开磁场的时间t。

2、计算题  如图所示在平面直角坐标系xOy中，，第Ⅰ、II象限存在沿y轴负方向的匀强电场，场强大小为E，第III、Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B．一质量为m、电荷量为q的带正电的粒子从y轴正半轴上距原点O为d的P点以速度v0垂直于y轴射入第Ⅰ象限的电场，经x轴射入磁场，已知，．不计粒子重力，求：

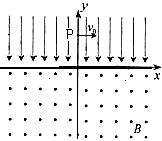
（1）粒子在磁场中运动的半径，画出带电粒子运动的轨迹。
（2）从粒子射入电场开始，求粒子经过x轴时间的可能值。

3、选择题  一带电荷量为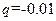C的质点，只受到重力、电场力和空气阻力三个力作用，由空中的a点运动到b点，重力势能增加3J，克服空气阻力做功0.5J，机械能增加0.5J，则下列判断正确的是
A．a、b两点间的电势差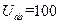V
B．质点的动能减少2.5J
C．空间电场一定是匀强电场
D．若空间还存在匀强磁场，则质点一定是做曲线运动

4、简答题  带电量为q的粒子（不计重力），匀速直线通过速度选择器（电场强度为E，磁感应强度为B1），又通过宽度为l，磁感应强度为B2的匀强磁场，粒子离开磁场时速度的方向跟入射方向间的偏角为θ，如图所示.试证明：入射粒子的质量m=.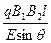

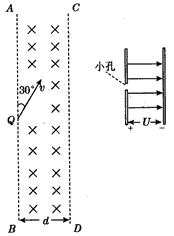
5、计算题  如图所示，在空间中存在垂直纸面向里的场强为B匀强磁场，其边界AB、CD的宽度为d，在左边界的Q点处有一质量为m，带电量为负q的粒子沿与左边界成30°的方向射入磁场，粒子重力不计。求：
（1）带电粒子能从AB边界飞出的最大速度？
（2）若带电粒子能垂直CD边界飞出磁场，穿过小孔进入如图所示的匀强电场中减速至零且不碰到负极板，则极板间电压及整个过程中粒子在磁场中运动的时间？
（3）若带电粒子的速度是（2）中的倍，并可以从Q点沿纸面各个方向射入磁场，则粒子能打到CD边界的范围？