1、计算题  (12分)一匀强磁场分布在以O为圆心，半径为R的圆形区域内，方向与纸面垂直，如图所示，质量为m、电荷量q的带正电的质点，经电场加速后，以速度v沿半径MO方向进入磁场，沿圆弧运动到N点，然后离开磁场，∠MON=120?，质点所受重力不计，求：

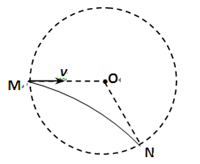
(1)判断磁场的方向；
(2)该匀强磁场的磁感应强度B；
(3)带电质点在磁场中运动的时间。

2、简答题  如图所示，为显像管电子束偏转示意图，电子质量为m，电量为e，进入磁感应强度为B的匀强磁场中，该磁场束缚在直径为l的圆形区域，电子初速度v0的方向过圆形磁场的轴心O，轴心到光屏距离为L（即P0O=L），设某一时刻电子束打到光屏上的P点，求PP0之间的距离．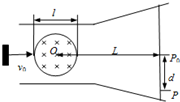

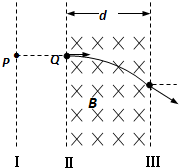
3、简答题  如图所示，Ⅰ、Ⅱ、Ⅲ为电场和磁场的理想边界，一束电子（电量为e，质量为m，重力不计）由静止状态从P点经过Ⅰ、Ⅱ间的电场加速后垂直到达边界Ⅱ的Q点．匀强磁场的磁感应强度为B，磁场边界宽度为d，电子从磁场边界Ⅲ穿出时的速度方向与电子原来的入射方向夹角为30°．求：
（1）电子在磁场中运动的时间t；
（2）若改变PQ间的电势差，使电子刚好不能从边界Ⅲ射出，则此时PQ间的电势差U是多少？

4、其他  ）如图所示，水平面内有两根互相平行且足够长的光滑金属轨道，它们间的距离L="0.20" m，在两轨道的左端之间接有一个R=0.10W的电阻.在虚线OO

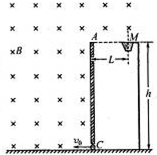
5、简答题  如图所示，水平绝缘地面上有一底部带有小孔的绝缘弹性竖直挡板AC，板高h=9cm，与A端等高处有一水平放置的篮筐，圆形筐口的圆心M离挡板的距离L=3m，AC左端及A端与筐口的连线上方存在匀强磁场和匀强电场，磁场方向垂直纸面向里，磁感应强度B=1T；现有一质量m=1×10-3kg、电量q=-1×10-3C、直径略小于小孔宽度的带电小球（视为质点），以某一速度从C端水平射入场中做匀速圆周运动．若球可直接从M点落入筐中，也可与AC相碰后从M点落入筐中，且假设球与AC相碰后以原速率沿碰前速度的反方向弹回弹回，碰撞时间不计，碰撞时电荷量不变，忽略小球运动对电场、磁场的影响．（g=10m/s2，sin53°=0.8），求：
（1）电场强度的大小与方向；
（2）小球运动的最大速率；
（3）若小球与AC碰撞1次后从M点落入筐中，求小球在电场和磁场共存的区域运动的时间（结果中可保留π）．