1、简答题  如图所示，y轴在竖直方向，x轴在水平方向，一质量为m，带电量为q的小球在座标为（0，0.3）A点以初速度v0平行于x轴正方向射入电场中，在y>0，x>0的空间存在沿y轴负方向的匀强电场E1，在y<0，x>0的空间存在沿x轴负方向的匀强电场E2，其中m=0.1kg，q=" +" 1.0×10-3C，v0=2m/s,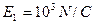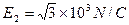，，重力加速度g=10m/s2，求：
（1）小球到达x轴上的速度
（2）小球回到y轴时的座标

2、简答题  

（1）微粒从A到P所经历的时间和加速度的大小；

3、计算题  如图甲所示，在两平行金属板的中线OO′某处放置一个粒子源，粒子沿OO1方向连续不断地放出速度的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场，磁感应强度B=0.01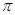T，方向垂直纸面向里，MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比，粒子的重力和粒子之间的作用力均可忽略不计，若时刻粒子源放出的粒子恰能从平行金属板边缘离开电场（设在每个粒子通过电场区域的时间内，可以把板间的电场看作是恒定的）。求：

（1）时刻粒子源放出的粒子离开电场时的速度大小和方向。
（2）从粒子源放出的粒子在磁场中运动的最短时间和最长时间。

4、简答题  如图所示，在竖直平面内有水平向右的匀强电场，场强为．同时存在水平方向垂直电场方向向内的匀强磁场，磁感应强度B＝1T．现有一带电粒子质量，带电量为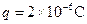，它在竖直平面内做直线运动．．

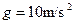　　（1）分析带电粒子的运动方向和速度的大小；
　　（2）当带电粒子运动到某一点A时突然撒去磁场，求带电粒子运动到与A点在同一水平线上的B点所需的时间t．

5、选择题  图为示波管的原理图，如果在电极YY′之间所加的电压按图甲所示的规律变化，在电极XX′之间所加的电压按图乙所示的规律变化，则在荧光屏上会看到的图形是 （ ）