1、简答题 如图所示,y轴在竖直方向,x轴在水平方向,一质量为m,带电量为q的小球在座标为(0,0.3)A点以初速度v0平行于x轴正方向射入电场中,在y>0,x>0的空间存在沿y轴负方向的匀强电场E1,在y<0,x>0的空间存在沿x轴负方向的匀强电场E2,其中m=0.1kg,q=" +" 1.0×10-3C,v0=2m/s,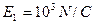 ,
,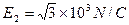 ,重力加速度g=10m/s2,求:
,重力加速度g=10m/s2,求:
(1)小球到达x轴上的速度
(2)小球回到y轴时的座标
参考答案:(1)V=4m/s(2)(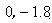 )
)
本题解析:①(8分)小球做类平抛运动,设在竖直方向加速度为a1,运动时间为t,未速度为V,V与x轴正方向夹角α
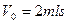
 ?……?①
?……?①
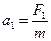 ?……?②
?……?②
 ?……?③
?……?③
 ?……?④
?……?④
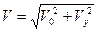 ?……?⑤
?……?⑤
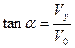 ?……?⑥
?……?⑥
由以上各式得V=4m/s,α=60°
①②③④⑤⑥各式1分,答案2分
 ②(12分)由受力分析可知小球再次做类平抛运动,设运动的加速度为a2,x1为第一次水平方向的位移,运动轨迹如图所示:
②(12分)由受力分析可知小球再次做类平抛运动,设运动的加速度为a2,x1为第一次水平方向的位移,运动轨迹如图所示:
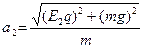 ?……⑦
?……⑦

 ?……⑧
?……⑧
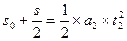 ?……⑨
?……⑨
 ?……⑩
?……⑩
 ?……11
?……11

⑦2分⑧1分,⑨⑩⑾各2分,答案3分
本题难度:一般
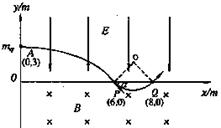
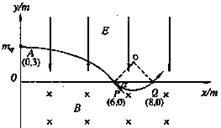
2、简答题

(1)微粒从A到P所经历的时间和加速度的大小;
(2)求出微粒到达P点时速度方向与x轴正方向的夹角,并画出带电微粒在电、磁场中
由A至Q的运动轨迹;
(3)电场强度E和磁感强度B的大小.
参考答案:
(1)0.05s 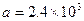 m/s2
m/s2
(2)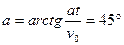
(3)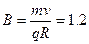
本题解析:(1)微粒从平行 轴正方向射入电场区域,由A到P做类平抛运动,微粒沿
轴正方向射入电场区域,由A到P做类平抛运动,微粒沿 轴方向做匀速直线运动
轴方向做匀速直线运动
本题难度:一般
3、计算题 如图甲所示,在两平行金属板的中线OO′某处放置一个粒子源,粒子沿OO1方向连续不断地放出速度 的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场,磁感应强度B=0.01
的带正电的粒子。在直线MN的右侧分布有范围足够大的匀强磁场,磁感应强度B=0.01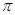 T,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比
T,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板间的电压U随时间变化的U—t图线如图乙所示。已知带电粒子的荷质比 ,粒子的重力和粒子之间的作用力均可忽略不计,若
,粒子的重力和粒子之间的作用力均可忽略不计,若 时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:
时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:

(1) 时刻粒子源放出的粒子离开电场时的速度大小和方向。
时刻粒子源放出的粒子离开电场时的速度大小和方向。
(2)从粒子源放出的粒子在磁场中运动的最短时间和最长时间。
参考答案:(1)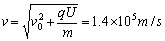 θ=45°(2)
θ=45°(2)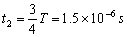

本题解析:(1)设板间距为d,t=0.1s时刻释放的粒子在板间做类平抛运动
在沿电场方向上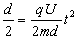 ①
①
粒子离开电场时,沿电场方向的分速度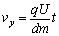 ②
②
粒子离开电场时的速度 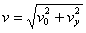 ③
③
粒子在电场中的偏转角为θ 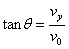 ④
④
由①②③④得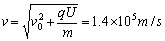
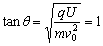 θ=45°
θ=45°
说明:用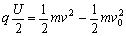 和
和 联立求出正确结果,参照上述评分标准给分。
联立求出正确结果,参照上述评分标准给分。
(2)带电粒子在匀强磁场中做匀速圆周运动的周期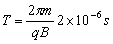
不同时刻释放的粒子在电场中的偏转角θ不同,进入磁场后在磁场中运动的时间不同,θ大的在磁场中的偏转角大,运动时间长。
t=0时刻释放的粒子,在电场中的偏转角为0,在磁场中运动的时间最短:

t=0.1s时刻释放的粒子,在电场中的偏转角最大为45°,在磁场中运动的时间最长:
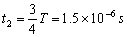
考点:考查了带电粒子在电磁场中的运动
点评:本题关键是画出粒子进入磁场后的各种可能的运动轨迹,根据洛伦兹力提供向心力列式后得出半径,然后求出磁偏转的距离表达式,并得出回旋角度的范围,从而得到磁偏转的范围.
本题难度:一般
4、简答题 如图所示,在竖直平面内有水平向右的匀强电场,场强为 .同时存在水平方向垂直电场方向向内的匀强磁场,磁感应强度B=1T.现有一带电粒子质量
.同时存在水平方向垂直电场方向向内的匀强磁场,磁感应强度B=1T.现有一带电粒子质量 ,带电量为
,带电量为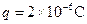 ,它在竖直平面内做直线运动.
,它在竖直平面内做直线运动.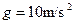 .
.

(1)分析带电粒子的运动方向和速度的大小;
(2)当带电粒子运动到某一点A时突然撒去磁场,求带电粒子运动到与A点在同一水平线上的B点所需的时间t.
参考答案:(1)v的方向与E的方向成j=60° (2)
(2)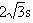
本题解析:(1)带电粒子在竖直平面内做直线运动,三力的合力必为零.
重力 ,竖直向下.电场力
,竖直向下.电场力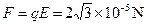 ,水平向右.
,水平向右.
G与F的合力 .方向q =arctan
.方向q =arctan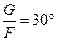
R与f为平衡力,f=Bqv=R  .v与R垂直,R与E成30°角,故v的方向与E的方向成j=60°.
.v与R垂直,R与E成30°角,故v的方向与E的方向成j=60°.
(2)去掉磁场B后,由A到B,做类平抛运动,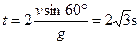 .
.
本题难度:一般
5、选择题 图为示波管的原理图,如果在电极YY′之间所加的电压按图甲所示的规律变化,在电极XX′之间所加的电压按图乙所示的规律变化,则在荧光屏上会看到的图形是 ( )


参考答案:C
本题解析:因为在电极xx′之间所加的电压保持不变,可知在x方向上的偏转位移保持不变,在y方向上电压随正弦规律变化,即y方向上偏移在正负最大值之间变化.故C正确,ABD错误.故选:C.
考点:示波管的原理
本题难度:一般