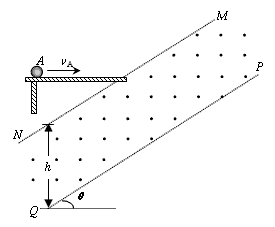
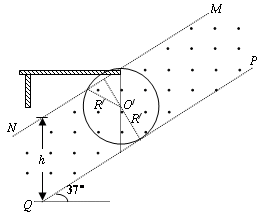
1、计算题  如图所示，光滑的绝缘平台水平固定，在平台右下方有相互平行的两条边界MN与PQ，其竖直距离为h=1.7m，两边界间存在匀强电场和磁感应强度为B=0.9T且方向垂直纸面向外的匀强磁场，MN过平台右端并与水平方向呈θ=37°．在平台左端放一个可视为质点的A球，其质量为mA=0.17kg，电量为q=+0.1C，现给A球不同的水平速度，使其飞出平台后恰好能做匀速圆周运动．g取10m/s2．
（1）求电场强度的大小和方向；
（2）要使A球在MNPQ区域内的运动时间保持不变，则A球的速度应满足的条件？（A球飞出MNPQ区域后不再返回）
（3）在平台右端再放一个可视为质点且不带电的绝缘B球，A球以vA0=3m/s的速度水平向右运动，与B球碰后两球均能垂直PQ边界飞出，则B球的质量为多少？

参考答案：解： (1)A球能做圆周运动，必须有：Eq=mAg

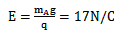
电场强度方向竖直向上
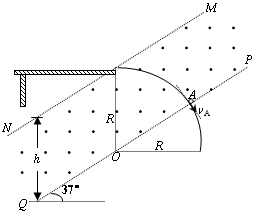
(2)A球在MNPQ区域运动时间相等，必须从边界MN飞出，如图所示，最大半径满足：R"cosθ+R"=hcosθ
A球做匀速圆周运动有：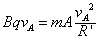
解得：vA=0.4m/s
依题意，A球速度必须满足：0＜vA≤0.4m/s
(3)AB相碰后，A做匀速圆周运动，半径R=h
由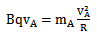得vA=0.9m/s
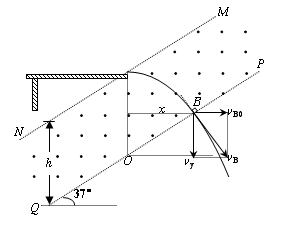
B球做平抛运动，设飞行的水平距离为x，时间为t，有：
x=vB0t

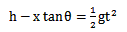
vB0=vytanθ=gttanθ
得vB0=3m/s
由动量守恒定律得：
mAvA0=mAvA+mBvB0
mB=0.119Kg。

本题解析：

本题难度：困难

2、选择题  两个带正电的离子被加速后，沿着一条直线相向运动而发生猛烈碰撞，若要碰撞前的动能尽可能多地转化为内能，应该设法使两个离子在碰撞前具有（　　）
A．大小相等的动量
B．大小相等的速度
C．相同的动能
D．相同的电荷量

参考答案：碰撞后尽可能多的动能转化为内能，也就是在碰撞过程中损失的机械能尽可能多，在完全非弹性碰撞中，碰撞后两粒子粘在一起时，粒子损失的机械能最多．而在碰撞过程中遵循动量守恒定律可知，碰撞前系统的总动量为零则碰撞后系统的总动量亦为零，所以本题关键是设法使这两个重离子在碰撞前瞬间具有大小相等方向相反的动量，这样可以保证碰撞后粒子的动能最小．
故选A

本题解析：

本题难度：简单

3、选择题  劲度系数为k的轻弹簧的一端固定在墙上，另一端和质量为M的容器放在光滑水平面上。开始时将弹簧压缩Lo，然后撤去外力，使容器绕O往复运动，在O的上方有一滴管，容器每通过O点一次，就有质量为m的一个液滴落入容器，则（?）

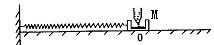
A．弹簧、容器(包括液滴)系统机械能守恒
B．液滴落入容器的短暂时间内系统水平方向动量守恒
C．容器振动的振幅逐渐减小
D．容器振动的周期逐渐增加

参考答案：
BCD

本题解析：略

本题难度：简单

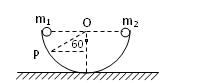
4、选择题  半圆形光滑轨道固定在水平地面上，如图4所示，并使其轨道平面与地面垂直，物体m1、m2同时由轨道左、右最高点释放，二者碰后粘在一起向左运动，最高能上升到轨道P点，已知OP与竖直方向夹角为60°，则两物体的质量之比m1∶m2为：?（?）

A．∶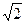
B．∶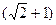
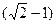
C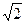．∶1
D．∶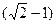

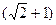
参考答案：D

本题解析：略

本题难度：简单

5、实验题  质量为m的球A在通过如图6-9所示半径为R的光滑圆轨道最高点时，对轨道的压力是其重力的2倍，则小球应从h=___________的光滑轨道滚下.

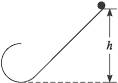
图6-9

参考答案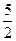：R

本题解析：mg+2mg= mv2/R
mg(h-2R)=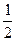mv2,
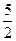解得h=R.

本题难度：简单