1、简答题  在近似计算时，可以把地球绕太阳公转看做是匀速圆周运动，平均半径为1.5×1011m，则可以算出太阳的质量大约为多少？（G=6.7×10-11N．m2/kg2）

2、计算题  据报道，最近在太阳系外发现了首颗“宜居”行星，其质量约为地球质量的6.4倍，其半径r约为地球半径的2倍，假设有一艘飞船环绕该星球做匀速圆周运动，且飞行速度为v=8km/s。(地球的半径R=6400km ，地球表面的重力加速度g=10m/s2)求：
（1）该行星表面的重力加速度：
（2）飞船到该星球表面的距离。( 结果保留2位有效数字)

3、计算题  （10分）2005年10月12日上午9时，“神州”六号载人飞船发射升空。火箭点火起飞，588秒后，飞船与火箭分离，准确入轨，进入椭圆轨道运行。飞船飞行到第5圈实施变轨，进入圆形轨道绕地球飞行。设“神州”六号飞船质量为m，当它在椭圆轨道上运行时，其近地点距地面高度为h1，飞船速度为v1，加速度为a1；在远地点距地面高度为h2，飞船速度为v2．已知地球半径为R（如图所示），求飞船

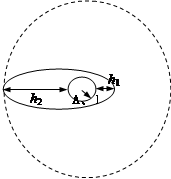
（1）由远地点到近地点万有引力所做的功
（2）在远地点的加速度a2

4、选择题  教科版高中物理教材必修2中介绍, ,亚当斯通过对行星“天王星”的长期观察发现，其实际运行的轨道与圆轨道存在一些偏离，且每隔时间t发生一次最大的偏离。亚当斯利用牛顿发现的万有引力定律对观察数据进行计算, 认为形成这种现象的原因可能是天王星外侧还存在着一颗未知行星（后命名为海王星），它对天王星的万有引力引起其轨道的偏离。由于课本没有阐述其计算的原理，这极大的激发了树德中学天文爱好社团的同学的探索热情，通过集体研究，最终掌握了亚当斯当时的计算方法：设其（海王星）运动轨道与天王星在同一平面内，且与天王星的绕行方向相同，天王星的运行轨道半径为R，周期为T，并认为上述最大偏离间隔时间t就是两个行星相邻两次相距最近的时间间隔，并利用此三个物理量推导出了海王星绕太阳运行的圆轨道半径，则下述是海王星绕太阳运行的圆轨道半径表达式正确的是（?）
A．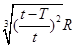
B．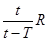
C．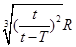
D．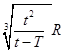

5、选择题  潮汐现象主要是由于月球对地球的不同部分施加不同的万有引力而产生的．可以近似认为地球表面均有水覆盖，如果地球与月球的相对位置如图所示，则在图中a、b、c、d四点中（　　）
A．a点处于高潮，c点处于低潮
B．b点既不处于高潮也不处于低潮
C．c点处于高潮，d点处于低潮
D．d点处于高潮，c点处于低潮