1、选择题  物体沿光滑固定斜面向下加速滑动，在运动过程中，下述说法正确的是

[? ]

参考答案：C

本题解析：

本题难度：简单

2、计算题  （16分）如图所示，A、B两球质量均为m，其间有压缩的轻短弹簧处于锁定状态。弹簧的长度、两球的大小均可忽略，整体视为质点。该装置从半径为R的竖直光滑圆轨道左侧与圆心等高处由静止下滑，滑至最低点时，解除对弹簧的锁定状态之后，B球恰好能到达轨道最高点，求：

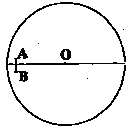
（1）滑至最低点时，解除对弹簧的锁定状态之前A球和B球的速度v0的大小。
（2）最低点时，解除对弹簧的锁定状态之后A球和B球速度vA和vB的大小。
（3）弹簧处于锁定状态时的弹性势能。

参考答案：???

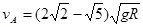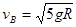本题解析：设A、B系统滑到圆轨道最低点时锁定为V0，解除弹簧锁定后A、B的速度分别为vA、vB，B到轨道最高点的速度为v，则有：
（1）根据系统机械能守恒有：?得：??（1分）?
（2）对B，在最高点重力提供向心力有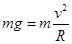： ?（2分）
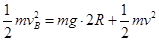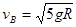解除锁定后在最低点由系统机械能守恒：?（2分） ?（1分）
对A.B组成系统由动量守恒有：?（3分）?
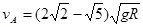?（1分）
（3）由系统机械能守恒有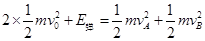：?（2分）?
解得：?（1分）

本题难度：一般

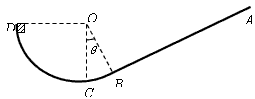
3、计算题  如图所示，粗糙斜面AB与竖直平面内的光滑圆弧轨道BCD相切于B点，圆弧轨道的半径为R，C点在圆心O的正下方，D点与圆心O在同一水平线上，∠COB=θ。现有质量为m的物块从D点无初速释放，物块与斜面间的动摩擦因数为μ，重力加速度为g。求：
（1）物块第一次通过C点时对轨道压力的大小；
（2）物块在斜面上运动离B点的最远距离。

参考答案：解：（1）物块从D到C，根据机械能守恒定律，得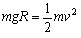
物块经C点，根据牛顿第二定律，得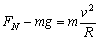
由以上两式得支持力大小FN=3mg
由牛顿第三定律得，物块对轨道的压力大小为3mg
（2）小物体通过圆弧轨道后，在斜面上运动到最大距离S时速度为0，由动能定理可得

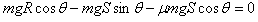
故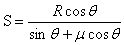

本题解析：

本题难度：一般

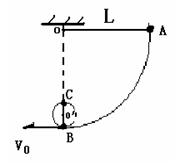
4、计算题  (8分)如下图所示，质量为m的小球由长为L的轻绳固定在O点，今将小球拉至水平A点静止释放 ，在O点正下方何处钉一铁钉O′方能使小球绕O′点在竖直平面内做圆周运动?
?

参考答案：0.6L

本题解析：设小园的半径为r,恰好到C点，则有mg=mvc2/r?①
A-C由机械能守恒得：mgL=mvc2/2 +2mgr?②
由①②得，rmin=0.4L,00/max=0.6L
本题考查机械能守恒定律的应用和圆周运动规律的应用，在c 点刚好通过的临界条件为只有重力提供向心力，在从A点到C点由动能定律可求得C点速度

本题难度：一般

5、选择题  如图所示,固定在竖直平面内的光滑3/4圆弧轨道AB-CD,其A点与圆心等高,D点为轨道最高点,AC为圆弧的一条水平直径,AE为水平面.现使小球自A点正上方O点处静止释放,小球从A点进入圆轨道后能通过轨道最高点D.则(? )

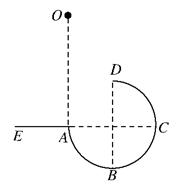
A.小球通过D点时速度可能为零
B.小球通过D点后,一定会落到水平面AE上
C.小球通过D点后,一定会再次落到圆轨道上
D.O点可能与D点等高

参考答案：B

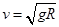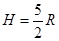本题解析：由竖直面内圆周运动规律可知:小球既然能通过最高点则过最高点时速度不可能为零,其临界速度为,其中R为光滑圆弧轨道的半径.由机械能守恒可得小球要通过最高点D,至少应从处开始下落,因此AD错误;若小球刚好可以通过D点,则离开D点后做平抛运动,当下落R高度时,需要时间为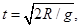其水平位移为大于圆轨道的半径,故小球一定不会落到圆轨道上,只能落在水平面AE上,C错误;B正确.

本题难度：简单