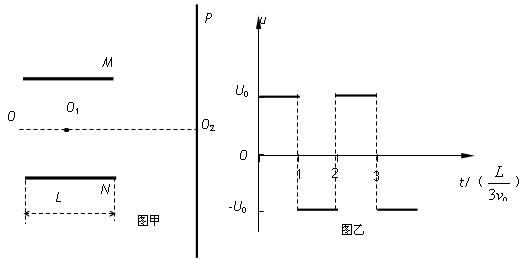
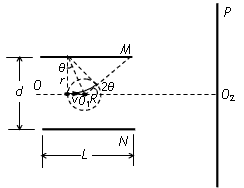
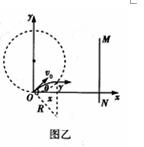
1、计算题  如图甲所示，M和N是相互平行的金属板，OO1O2为中线，O1为板间区域的中点，P是足够大的荧光屏，带电粒子连续地从O点沿OO1方向射入两板间。
（1）若只在两板间加恒定电压U，M和N相距为d，板长为L（不考虑电场边缘效应）。若入射粒子是电量为e、质量为m的电子，试求能打在荧光屏P上偏离点O2最远的电子的动能。
（2）若两板间只存在一个以O1点为圆心的圆形匀强磁场区域，磁场方向垂直纸面向里，已知磁感应强度B=0.50T，两板间距d=cm，板长L=1.0cm，带电粒子质量m=2.0×10-25 kg，电量q=8.0×10-18 C，入射速度v=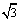×105m/s。若能在荧光屏上观察到亮点，试求粒子在磁场中运动的轨道半径r，并确定磁场区域的半径R应满足的条件。
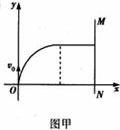
（3）若只在两板间加如图乙所示的交变电压u，M和N相距为d，板长为L（不考虑电场边缘效应）。入射粒子是电量为e、质量为m的电子。某电子在t0=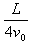时刻以速度v0射入电场，要使该电子能通过平行金属板，试确定U0应满足的条件。

参考答案：解：（1）电子在两极板间的加速度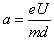
通过金属板的时间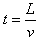
对打在荧光屏P上偏离点O2最远的粒子有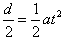
此时粒子的动能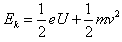
联列解得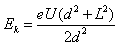
（2）由牛顿第二定律可知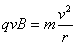
代入数据解得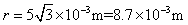
如图所示，设恰好在荧光屏P上观察到亮点时，粒子偏转角为2θ，磁场区域的最大半径为R0，由几何关系可知，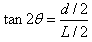

代入数据解得
则R应满足的条件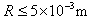
（3）交变电压的周期，则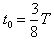
电子通过金属板的时间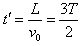
电子在两极板间的加速度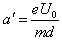
设电子分别在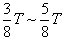、、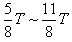、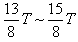时间内沿垂直于初速度方向运动的位移依次为y1、y2、y3、y4，则有



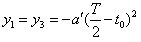
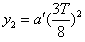
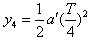
要使电子能通过平行金属板，应满足条件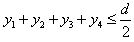
联列解得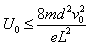

本题解析：

本题难度：困难

2、简答题  如图所示，质量为m．电荷量为e的电子从坐标原点0处沿xOy平面射人第一象限内，射入时的速度方向不同，但大小均为v0．已知包括原点O在内的圆形区域内有方向垂直于xOy平面向里的匀强磁场，磁感应强度大小为B，这些电子穿出磁场后都能垂直打在与y轴平行的荧光屏MN上，屏MN与y轴间的距离等于电子在磁场中做圆周运动的半径的2倍（不计电子的重力以及电子间相互作用）．
（1）在O点沿y轴正方向进入磁场的电子经多长时间打在屏上？
（2）若电子穿出磁场时的位置坐标为（x，y），试写出x与y应满足的方程式，并分析指出圆形磁场区的圆心位置坐标和半径；
（3）求这些电子在磁场中运动范围的面积．

参考答案：





（1）设电子做圆周运动的半径为R，
由牛顿第二定律可得，ev0B=mv20R
解得：R=mv0eB
?电子做圆周运动的周期：T=2πmeB
沿y轴正方向进入磁场的电子运动轨迹，如图甲所示．
电子在磁场中运动的时间：t1=T4=πm2eB
电子穿出磁场后的运动时间：t2=2R-Rv0=meB
所以该电子运动的时间：t=t1+t2=(π+2)m2eB
（2）入射方向与x轴正方向夹角为θ的电子轨迹，如图乙所示，
电子穿出磁场时的位置坐标为（x，y），
由图乙可得：x2+（R-y）2=R2，
即x2+(y-mv0eB)2=(mv0eB)2
电子穿出磁场的位置在磁场圆的圆周上，故磁场圆周圆心坐标为（0，mv0eB）
磁场圆半径等于轨迹圆半径为r=R=mv0eB
磁场圆如图乙所示中虚线圆所示．
（3）这些电子在磁场中的运动范围由图丙所示的两段圆弧围成，
面积等于图中阴影面积的2倍，即：S=2?(πR24-R22)=π-22(mv0eB)2
答：
（1）在O点沿y轴正方向进入磁场的电子经(π+2)m2eB时间打在屏上；
（2）若电子穿出磁场时的位置坐标为（x，y），则x与y应满足的方程式，并分析指出圆形磁场区的圆心位置坐标（0，mv0eB）和半径mv0eB；
（3）则这些电子在磁场中运动范围的面积π-22(mv0eB)2．

本题解析：

本题难度：一般

3、选择题  如图所示，Ⅰ、Ⅱ、Ⅲ是竖直平面内三个相同的半圆形光滑轨道，K为轨道最低点，Ⅰ处于匀强磁场中，Ⅱ和Ⅲ处于匀强电场中，三个完全相同的带正电小球a、b、c从轨道最高点自由下滑至第一次到达最低点K的过程中，下列说法正确的是（　　）

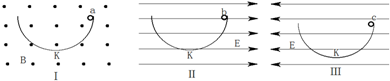
A．在K处球a速度最大
B．在K处球b对轨道压力最大
C．球b需要的时间最长
D．球c机械能损失最多

参考答案：对a小球受力分析可知，Fa+qvB-mg=mva2r，所以Fa=mg-qvB+mva2r；
对b球受力分析可得，Fb-mg=mvb2r，所以Fb=mg+mvb2r；
对c球受力分析可知，Fc-mg=mvc2r，所以Fc=mg+mvc2r；
由于a球在磁场中运动，磁场力对小球不做功，整个过程中小球的机械能守恒；
b球受到的电场力对小球做负功，到达最低点时的速度的大小最小，所以b球的运动的时间也长，所以A错误C正确；
c球受到的电场力对小球做正功，到达最低点时球的速度大小最大，所以c球的机械能增加，c球对轨道压力最大，所以B错误，D错误．
故选：C．

本题解析：

本题难度：简单

4、选择题  如图所示，在OA和OC两射线间存在着匀强磁场，∠AOC为30°，正负电子(质量、电荷量大小相同，电性相反）以相同的速度均从M点以垂直于OA的方向垂直射入匀强磁场，下列说法可能正确的是

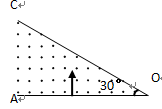
A．若正电子不从OC 边射出，正负电子在磁场中运动时间之比可能为3∶1
B．若正电子不从OC 边射出，正负电子在磁场中运动时间之比可能为6∶1
C．若负电子不从OC 边射出，正负电子在磁场中运动时间之比可能为1∶1
D．若负电子不从OC 边射出，正负电子在磁场中运动时间之比可能为1∶6