1、简答题  如图所示，在某空间实验室中，有两个靠在一起的等大的圆柱形区域，分别存在着等大反向的匀强磁场，磁感应强度B=0.10T，磁场区域半径r=

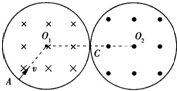
参考答案：

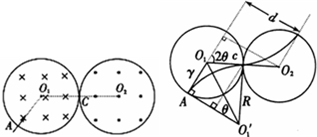
（1）离子在磁场中做匀速圆周运动，在左右两区域的运动轨迹是对称的，
如右图，设轨迹半径为R，圆周运动的周期为T，
由牛顿第二定律得，Bqv=mv2R，又因：T=2πRv，联立可得，R=mvBq? T=2πRBq
解得：R=2m，
由轨迹图知，tanθ=rR=

本题解析：

本题难度：一般

2、计算题  汽车以10m/s的速度通过一座拱桥的最高点，拱桥半径20m，求此车里的一名质量为20kg的小孩对座椅的压力。（g=10m/s2）

参考答案：mg－FN=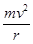
FN=100N
小孩对座椅的压力为100N

本题解析：mg－FN=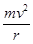
FN=100N
小孩对座椅的压力为100N

本题难度：简单

3、计算题  如图所示水平转盘上放有质量为m的物块，物块到转轴上O点的距离为r, 物块和转盘间最大静摩擦力是压力的μ倍。求：

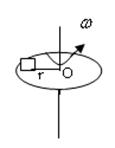
（1）若物块始终相对转盘静止，转盘转动的最大角速度是多少？
（2）用一水平细线将物块与转轴上的O点连接在一起，求当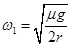时，细线的拉力T1和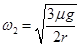时，细线的拉力T2。

参考答案：（1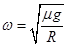）；（2）T1=0；T2 = μmg/2

本题解析：
试题分析: （1） 当物块所需要的向心力等于最大静摩擦力时，转盘角速度最大?即： μmg=" m" rωm2?
则:??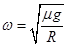
（2） 由于ω1 < ωm时仅由摩擦力可提供向心力，则细绳对物块的拉力T1=0。
由于ω2 > ωm时摩擦力不足以提供向心力，绳子也要提供部分向心力
则：T2 +μmg="m" rω22?
解得：T2 = μmg/2

本题难度：一般

4、填空题  甲、乙两个质点绕同一圆心做匀速圆周运动，甲的转动半径是乙的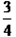，当甲转60周时乙转45周，甲、乙两个质点的向心加速度之比是______．

参考答案：4 : 3

本题解析：

本题难度：简单

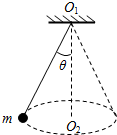
5、选择题  如图所示，一长为L的轻绳，一端固定在天花板上，另一端系一质量为m的小球，球绕竖直轴线O1O2在水平面内做匀速圆周运动，绳与竖直轴线间的夹角为θ，则下述说法中正确的是（　　）
A．小球受到重力、绳的拉力和向心力
B．小球的加速度大小为gtanθ
C．小球所需向心力大小为mgsinθ
D．小球运动的周期为2π

参考答案：A、小球受重力和绳的拉力两个力，两个力的合力提供向心力．故A错误．


B、根据F合=ma，F合=mgtanθ，解得a=gtanθ，故B正确．
C、小球所受的合力F合=mgtanθ，合力等于向心力等于mgtanθ．故C错误．
D、根据F合=mgtanθ=mr(2πT)2，r=Lsinθ．T=2π

本题解析：

本题难度：一般