1、填空题 有一行星密度为地球密度的一半,表面重力加速度为地球的2倍,则该行星质量为地球的_________倍,若地球同步卫星的高度为地球半径的6倍,该行星的同步卫星的高度为其半径的2.5倍,则该行星的自转周期为__________小时。
参考答案:32,12
本题解析:因为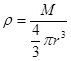 ,在星球表面有
,在星球表面有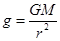 ,联立可得
,联立可得 ,
, 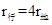
由公式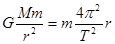 得
得 ,
,
点评:本题的计算量比较大,但是思路比较简单,需要细心计算
本题难度:简单
2、选择题 A和B是绕地球做匀速圆周运动的卫星,,A与B的轨道半径之比为1:2,则A与B的:
A.加速度之比为2∶1
B.周期之比为2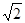 ∶1
∶1
C.线速度之比为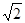 ∶ 1
∶ 1
D.角速度之比为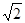 ∶1
∶1
参考答案:C
本题解析:人造地球卫星绕地球做匀速圆周运动时,万有引力提供向心力,据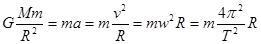 , aA :aB ="4" :1;周期之比为
, aA :aB ="4" :1;周期之比为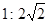 ;线速度之比为
;线速度之比为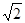 :1;角速度之比为
:1;角速度之比为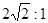
点评:本题难度较小,熟练掌握万有引力提供卫星圆周运动的向心力,并能写出向心力的不同表达式
本题难度:简单
3、选择题 已知引力常数G和下列各组数据,能计算出地球质量的是( )
A.地球绕太阳运行的周期及地球离太阳的距离
B.月球绕地球运行的周期及月球离地球的距离
C.人造地球卫星在地面附近绕行的速度及运行周期
D.若不考虑地球自转,己知地球的半径及重力加速度
参考答案:A、地球绕太阳运动的周期和地球与太阳的距离,根据万有引力提供向心力:GMmr2=m?4π2rT2其中m为地球质量,在等式中消去,只能求出太阳的质量M.也就是说只能求出中心体的质量.故A错误.
B、月球绕地球做匀速圆周运动,它受到地球的万有引力充当向心力,用它运动周期表示向心力,由万有引力定律结合牛顿第二定律得:GMmr2=m?4π2rT2
∴地球的质量M=4π2r3GT2,其中r为地球与月球间的距离,故B正确.
C、人造卫星绕地球做匀速圆周运动,它受到地球的万有引力充当向心力,用它运动周期表示向心力,
由万有引力定律结合牛顿第二定律得:GMmr2=m?4π2rT2
又因T=2πrv,
∴地球的质量M=Tv32πG,因此,可求出地球的质量,故C正确.
D、地球表面的物体受到的地球的重力等于万有引力,即mg=GMmr2,因此,可求出地球的质量M=gr2G,故D正确.
故选BCD.
本题解析:
本题难度:一般
4、计算题 (8分)1969年7月21日,美国宇航员阿姆斯特郎在月球上烙下了人类第一只脚印,迈出了人类征服宇宙的第一步,在月球上,如果阿姆斯特郎和同伴奥尔德林用弹簧测力计测出质量为m的仪器的重力为F。而另一位宇航员科林斯驾驶指挥舱,在月球表面飞行一周,记下时间T。只利用这些数据,计算出月球的质量。
参考答案: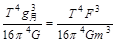
本题解析:能估算出月球的质量
由题意得 g=F/m?(2分)
在月球表面附近绕行时,有r=R?则
G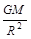 =ma向=mg月=mR
=ma向=mg月=mR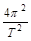 ?(2分)
?(2分)
得? M=g月R2/G
R=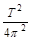 g月? 2分)
g月? 2分)
M=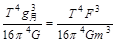 ?(2分。
?(2分。
本题难度:一般
5、选择题 在牛顿发现万有引力定律之后,测出引力常量的科学家是?
A.伽利略
B.卡文迪许
C.第谷
D.欧姆
参考答案:B
本题解析:在牛顿发现万有引力定律之后,测出引力常量的科学家是卡文迪许通过扭秤实验测的的
本题难度:简单