1、选择题 如图所示在一绝缘、粗糙且足够长的水平管道中有一带电量大小为q、质量为m的带电球体,管道半径略 大于球体半径。整个管道所在处存在磁感应强度为B的水平匀强磁场,磁感应强度方向垂直纸面向里,同 时存在竖直向下的匀强电场,电场强度为E。现给带电球体一个水平向右的初速度v0,则在以后的整个运动过程中,带电球体克服摩擦力所做的功可能为
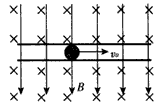
[? ]
A.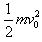
B.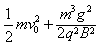
C.
D.
参考答案:ACD
本题解析:
本题难度:一般
2、计算题 如图所示,在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场:垂直纸面向外的匀强磁场I以及匀强磁场Ⅱ,O、M、P、Q为磁场边界和x轴的交点,MP区域是真空的,OM=MP=L。在第二象限存在沿x轴正向的匀强电场.一质量为m带电量为+q的带电粒子从电场中坐标为(-L,O)的点以速度v0沿+y方向射出,从y轴上坐标(O,2L) 的C处射入区域I,并且沿x的正方向射出区域I,带电粒子经过匀强磁场Ⅱ后第二次经过y,轴时就回到C点(粒子的重力忽略不计).求:
(1)第二象限匀强电场场强E的大小;
(2)区域I内匀强磁场磁感应强度B的大小;
(3)问区域Ⅱ内磁场的宽度至少为多少?
(4)粒子两次经过C的时间间隔为多少?
(5)请你通过对粒子运动轨迹描述定性判断:带电粒子能否通过坐标为(L,10L)的点.

参考答案:(1)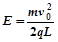 (2)
(2) (3)
(3)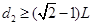
(4)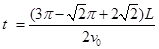 (5)否
(5)否
本题解析:(1)带电粒子在匀强电场中做类平抛运动.
根据类平抛规律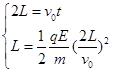 可求得
可求得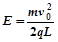 ?
?
(2)设到y轴时带电粒子的水平分速度为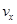 ,则
,则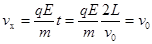 ?
?
粒子进入磁场Ⅰ的速度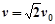 方向与x轴正向成450;
方向与x轴正向成450;
粒子进入区域Ⅰ做匀速圆周运动,由几何知识可得: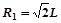 ?
?
由洛伦兹力充当向心力:
可解得: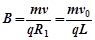 ?
?
(3)粒子在磁场区域Ⅱ做匀速圆周的半径为: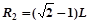 ,即只要满足
,即只要满足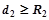 即可。
即可。
(4)粒子在磁场区域Ⅰ运动时间: ?
?
粒子在真空区域MP的运动时间: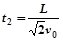
粒子在磁场区域Ⅱ运动时间: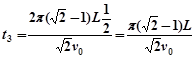 ?
?
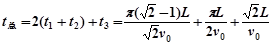
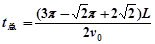 ?
?
(5)根据类平抛运动的对称性可知道:不能通过(L,10L)的点

点评:此类题型综合了物理学上重要的运动模型,通过结合类平抛运动规律,分析粒子进入磁场区域的速度大小和方向,并结合匀速圆周运动、几何知识求出磁场强度。在磁场区域1、真空区域、磁场区域2,由于粒子速度大小都不变,所以比较方便求出其返回C的时间。最后利用轨迹的对称性分析出不可能经过(L,10L)的点。
本题难度:一般
3、选择题 质量为m的带电小球在正交的匀强电场、匀强磁场中做匀速圆周运动,轨道平面在竖直平面内,电场方向竖直向下,磁场方向垂直圆周所在平面向里,如图所示,由此可知
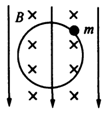
[? ]
A.小球带正电
B.小球带负电
C.沿逆时针方向运动
D.沿顺时针方向运动
参考答案:BD
本题解析:
本题难度:一般
4、简答题 如图所示,在图中第I象限的区域里有平行于y轴的匀强电场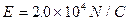 ,在第IV象限区域内有垂直于Oxy平面的匀强磁场B。
,在第IV象限区域内有垂直于Oxy平面的匀强磁场B。
带电粒子A,质量为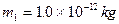 ,电量
,电量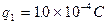 ,从y轴上A点以平行于x轴的速度
,从y轴上A点以平行于x轴的速度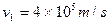 射入电场中,已知
射入电场中,已知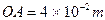 ,求:
,求:
(1)粒子A到达x轴的位置和速度大小与方向;
(2)在粒子A射入电场的同时,质量、电量与A相等的粒子B,从y轴上的某点B以平行于x轴的速度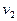 射入匀强磁场中,A、B两个粒子恰好在x轴上迎面正碰(不计重力,也不考虑两个粒子间的库仑力)试确定B点的位置和匀强磁场的磁感强度。
射入匀强磁场中,A、B两个粒子恰好在x轴上迎面正碰(不计重力,也不考虑两个粒子间的库仑力)试确定B点的位置和匀强磁场的磁感强度。
参考答案:(1)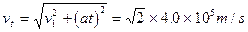
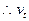 与x轴夹角:
与x轴夹角: (2)
(2)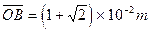
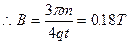
本题解析:(1)粒子A带正电荷,进入电场后在电场力作用下沿y轴相反方向上获得加速度,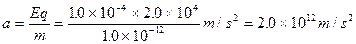
设A、B在x轴上P点相碰,则A在电场中运动时间可由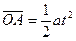 求解:
求解:
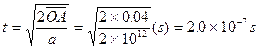
由此可知P点位置: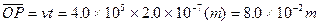
粒子A到达P点的速度,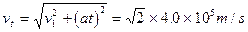
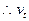 与x轴夹角:
与x轴夹角:
(2)由(1)所获结论,可知B在匀强磁场中作匀速圆周运动的时间也是 ,轨迹半径
,轨迹半径
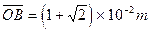
粒子B在磁场中转过角度为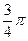 ,运动时间为
,运动时间为
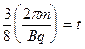 ?
?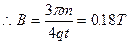
本题难度:简单
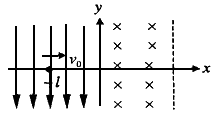
5、计算题 如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界;现有一个质量为m,电荷量为-q的带电粒子(不计重力),从电场中坐标位置(-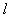 ,0)处以初速度v0沿x轴正方向开始运动,且已知
,0)处以初速度v0沿x轴正方向开始运动,且已知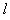 =
=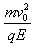 ,试求:
,试求:
(1)粒子第一次通过y轴时的位置?
(2)若要使带电粒子能穿越磁场区域而不再返回电场中,磁场的宽度d应满足的条件?
参考答案:解:(1)粒子在电场中飞行的时间为t,由水平方向匀速知:t=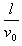
竖直方向: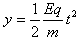
∴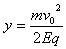
(2)设经过y轴的速度为v,由动能定理知: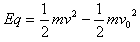
∴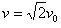
设与水平方向夹角为θ,则:cosθ=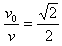
∴θ=45°
当粒子轨迹与磁场边界刚好相切时的磁场宽度为d0,则: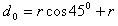
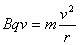
∴d0=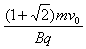
所以粒子不再飞回电场,磁场的宽度d<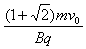
本题解析:
本题难度:困难