微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、简答题 如图所示,在光滑水平面上,质量为m的小球B连接着一个轻质弹簧,弹簧与小球均处于静止状态.质量为2m的小球A以大小为v0的水平速度向右运动,接触弹簧后逐渐压缩弹簧并使B运动,经过一段时间,A与弹簧分离.
(1)当弹簧压缩至最短时,弹簧的弹性势能EP为多大?
(2)若开始时,在B球的右侧某位置固定一块挡板,在A与弹簧未分离前使B球与挡板发生碰撞,并在碰撞后立即将挡板撤走.设B球与挡板碰撞时间极短,碰后B球的速度大小不变,但方向与原来相反.欲使此后弹簧被压缩到最短时弹簧的弹性势能能达到第(1)问中EP的2.5倍,必须使两球在速度达到多大时与挡板发生碰撞?
参考答案:(1)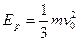 (2)
(2)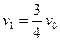 ?
?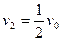
本题解析:(1)弹簧压缩至最短时,A、B速度均
为v,选取向右为正,根据动量守恒定律,有: ?
? ? 3分
? 3分
根据机械能守恒定律,有:
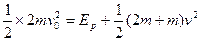 ?
?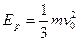 ? 3分
? 3分
(2)设B球与挡板碰撞时,A球速度为v1、B球速度为v2(均向右)
根据动量守恒定律: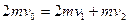 ? ——① ?2分
? ——① ?2分
此时弹簧弹性势?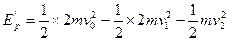 ? 3分
? 3分
则B球与挡板刚碰后:A球速度为v1、 B球速度为-v2(向左),此后
弹簧压缩至最短时共同速度为v3,则:
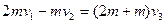 ? ——②?2分
? ——②?2分
此时弹簧弹性势能 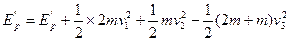
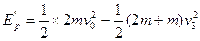 ?2分
?2分
由题意:?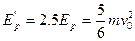 ?得
?得 ——③ 3分
——③ 3分
由①②③式可得: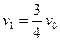 ?
?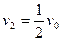 ?2分
?2分
本题难度:一般
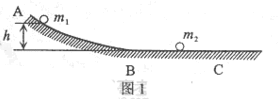
2、简答题 (1)如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为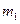 的小球从高位
的小球从高位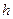 处由静止开始沿轨道下滑,与静止在轨道BC段上质量为
处由静止开始沿轨道下滑,与静止在轨道BC段上质量为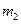 的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球
的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球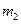 的速度大小
的速度大小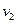 。
。
(2)碰撞过程中的能量传递规律在屋里学中有着广泛的应用。为了探究这一规律,我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的恶简化力学模型。如图2所示,在固定光滑水平轨道上,质量分别为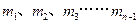 、
、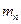 ……的若干个球沿直线静止相间排列,给第1个球初能
……的若干个球沿直线静止相间排列,给第1个球初能 ,从而引起各球的依次碰撞。定义其中第
,从而引起各球的依次碰撞。定义其中第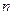 个球经过依次碰撞后获得的动能
个球经过依次碰撞后获得的动能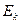 与
与 之比为第1个球对第
之比为第1个球对第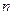 个球的动能传递系数
个球的动能传递系数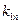 。
。
a.求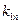 ;
;
b.若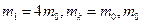 为确定的已知量。求
为确定的已知量。求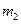 为何值时,
为何值时,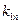 值最大。
值最大。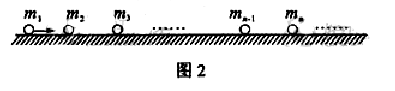
参考答案:(1)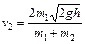
(2)a.
b.2m0
本题解析:
(1)设碰撞前的速度为,根据机械能守恒定律
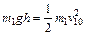 ?www.?①
?www.?①
设碰撞后m1与m2的速度分别为v1和v2,根据动量守恒定律
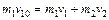 ?www.?②
?www.?②
由于碰撞过程中无机械能损失
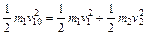 ?www.?③
?www.?③
②、③式联立解得
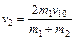 ?www.?④
?www.?④
将①代入得④
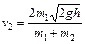 ?www.。
?www.。
(2)a由④式,考虑到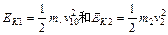 得
得
根据动能传递系数的定义,对于1、2两球
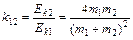 ?www.?⑤
?www.?⑤
同理可得,球m2和球m3碰撞后,动能传递系数k13应为
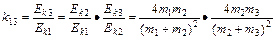 ?www.?⑥
?www.?⑥
依次类推,动能传递系数k1n应为
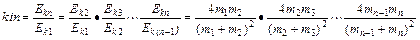 ?www.
?www.
解得
 ?www.
?www.
b.将m1=4m0,m3=mo代入⑥式可得
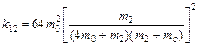
为使k13最大,只需使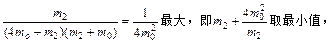
由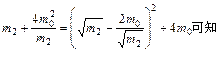
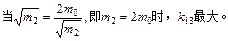
www.
本题难度:一般
3、选择题 两个带正电的离子被加速后,沿着一条直线相向运动而发生猛烈碰撞,若要碰撞前的动能尽可能多地转化为内能,应该设法使两个离子在碰撞前具有( )
A.大小相等的动量
B.大小相等的速度
C.相同的动能
D.相同的电荷量
参考答案:碰撞后尽可能多的动能转化为内能,也就是在碰撞过程中损失的机械能尽可能多,在完全非弹性碰撞中,碰撞后两粒子粘在一起时,粒子损失的机械能最多.而在碰撞过程中遵循动量守恒定律可知,碰撞前系统的总动量为零则碰撞后系统的总动量亦为零,所以本题关键是设法使这两个重离子在碰撞前瞬间具有大小相等方向相反的动量,这样可以保证碰撞后粒子的动能最小.
故选A
本题解析:
本题难度:简单
4、简答题 如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态,质量为2m的小球A以大小为v0的初速度向右运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离.
(1)当弹簧被压缩到最短时,弹簧的弹性势能Ep多大?
(2)若开始时在B球的右侧,某位置固定一挡板,在A球与弹簧未分离前使B球与挡板碰撞,并在碰后立刻将挡板撤走,设B球与挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反,欲使此后弹簧被压缩到最短时,弹性势能达到第(1)问中Ep的2.5倍,必须使B球的速度多大时与挡板发生碰撞?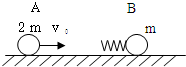
参考答案:(1)当弹簧压缩到最短时,A、B的速度相等,2mv0=3mv1 ①
A和B的共同速度v1=23v0
根据系统的机械能守恒得 12?2mv02=12?3mv12+Ep?②
解得 此时弹簧的弹性势能Ep=13mv02?③
(2)B碰挡板时没有机械能损失,碰后弹簧被压缩到最短时,A、B速度也相等,12?2mv02=12?3mv22+Ep′④
? Ep′=2.5Ep=56mv02
解得v2=±v03⑤
取向右为正方向.若v2=v03,则表示B球与板碰撞后,A、B此时一起向右运动.B球与板碰撞前B与A动量守恒
?2mv0=2?mvA+mvB⑥
B球与板碰撞后B与A动量也守恒
? 2mvA-mvB=3m?v03⑦
解得?vA=34v0,vB=v02
因为此时vA>vB,弹簧还将继续缩短,所以这种状态是能够出现的,
若v2=-v03,则表示B球与板碰撞后A、B向左运动,B球与板碰撞后B和A动量守恒
? 2mvA-mvB=3mv2=-3m?v03?⑧
由⑥⑧可得,vA=v04,vB=32v0?
此时A、B球的总动能EK总=12?2mvA2+12mvB2=m(v04)2+12(32v0)2=1916mv02?
EK总大于A球最初的动能mv02,因此vB=32v0这种状态是不可能出现的,因此必须使B球在速度为v02时与挡板发生碰撞.?⑨
答:
(1)当弹簧被压缩到最短时,弹簧的弹性势能Ep为13mv02.
(2)必须使B球在速度为v02时与挡板发生碰撞.
本题解析:
本题难度:一般
5、计算题 如图所示,足够长的光滑平台固定在水平地面上,平台中间放有小物体A和B,两者彼此接触.A的上表面是半径为R的半圆形轨道,轨道顶端距台面的高度为h处,有一个小物体C,A、B、C的质量均为m,在系统静止时释放C,已知在运动过程中 ,A、C始终接触,试求:
,A、C始终接触,试求:
(1)物体A和B刚分离时,B的速度.
(2)物体A和B分离后,C所能达到的距台面的最大高度.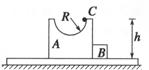
参考答案:(1)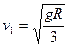 ?方向为水平向右
?方向为水平向右
(2)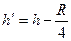
本题解析:(1)C滑至最低点时,A、B将分离。设此时A、B的速度为v1,C的速度为v2
A、B、C组成的系统水平方向动量守恒: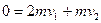 ……………………(2分)
……………………(2分)
A、B、C组成的系统机械能守恒: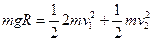 ……………………(2分)
……………………(2分)
此后B以v1的速度做匀速运动,且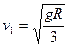 ?方向为水平向右……………………(1分)
?方向为水平向右……………………(1分)
(2)设C所能到达的最大高度为h?,此时A、C共速,依题意A、B分离后
A、C组成的系统水平方向动量守恒: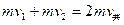
 …………………(2分)
…………………(2分)
A、B、C组成的系统机械能守恒: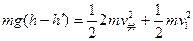 …………(2分)
…………(2分)
以上方程联立可得: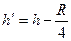 …………………(1分)
…………………(1分)
本题难度:简单