1、简答题  在水平面内的光滑平行导轨MM′、NN′长度为L，它们之间距离也是L，定值电阻R连接MN，导轨平面距地面高为h．在导轨所处空间有以M′N′为边界的竖直向上的匀强磁场．将长度为L，电阻为r的金属棒ab放在导轨M′N′端并使其恰好处在磁场的边界线内，如图甲所示．已知磁场与时间的关系如图乙所示（0＜t＜t1，B=Bo；t≥t1，B=B0-kt）．t1时刻磁场的减弱，使棒ab突然掉落在离轨道末端S远处的地面上．求金属棒抛离磁场瞬间回路的电热功率P．轨道电阻不计，重力加速度为g．

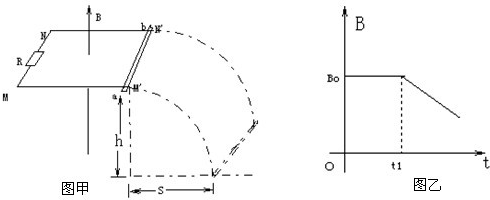
参考答案：设回路电流为i，所求电功率为P=i2（R+r）
由于i=e-BoLvR+r，
式中e=L2△B△t=L2k为B变化引起的感应电动势．
BoLv为棒切割磁感线引起的电动势，v=s

本题解析：

本题难度：一般

2、简答题  某一核反应的模型中质量为m0、速度为v0的粒子与一个质量为M、静止的原子核碰撞后合为一体，又迅速发生变化放出质量为m、速度为v的另一个粒子，此粒子的速度v与v0反方向.试问余下的反冲核的反冲速度为多大?

参考答案：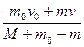

本题解析：由动量守恒定律得m0v0=(M+m0-m)v′-mv
余下的反冲核的反冲速度为v′=.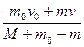

本题难度：简单

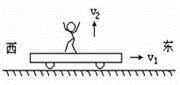
3、选择题  如图所示，质量为m的人立于平板车上，人与车的总质量为M，人与车以速度v1在光滑水平面上向东运动。当此人相对于车以速度v2竖直跳起时,车向东的速度大小为 ?（填选项前的字母）

A．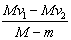　　　　
B．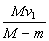　
C．　　
D．v1

参考答案：D

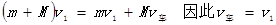
本题解析：试题分析： 在水平方向动量守恒，人向上跳起后，水平方向的速度没变，所以D正确。

本题难度：一般

4、简答题  如图所示，在光滑的水平地面上，静止着质量为M=2.0kg的小车A，小车的上表面距离地面的高度为0.8m，小车A的左端叠放着一个质量为m=1.0kg的小物块B（可视为质点）处于静止状态，小物块与小车上表面之间的动摩擦因数μ=0.20．在小车A的左端正上方，用长为R=1.6m的不可伸长的轻绳将质量为m=1.0kg的小球C悬于固定点O点．现将小球C拉至使轻绳拉直且与竖起方向成θ=60°角的位置由静止释放，到达O点的正下方时，小球C与B发生弹性正碰（碰撞中无机械能损失），小物块从小车右端离开时车的速度为1m/s，空气阻力不计，取g=10m/s2．求：
（1）小车上表面的长度L是多少？
（2）小物块落地时距小车右端的水平距离是多少？

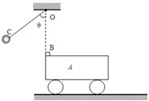
参考答案：（1）小球C向下摆动过程，只有重力做功，机械能守恒，则有：
mgR（1-cosθ）=12mv2，
解得C与B碰撞前的速度为：v=4m/s
C与B发生弹性正碰，两球组成系统动量和机械能都守恒，设碰后C、B的速度分别为v1和v2，选向右的方向为正，则得：
mv=mv1+mv2
12mv2=12mv21+12mv22
解得：v1=0，v2=4m/s
对于B在A上滑行过程，根据系统动量和能量守恒得：
mv2=mv3+Mv4，
μmgL=12mv22-12mv23-12Mv24
解得 L=2.5m，v3=2m/s
（2）小物块B离开小车后做平抛运动，则：
竖直方向：h=12gt2
水平方向：s1=v3t
此过程，小车做匀速运动，则得：
s2=v4t
故有：△s=s1-s2=0.4m．
答：（1）小车上表面的长度L是2.5m．
（2）小物块落地时距小车右端的水平距离是0.4m．

本题解析：

本题难度：一般

5、简答题  如图所示的凹形场地，两端是半径为L的光滑

参考答案：（1）设甲到达O处与乙碰撞前的速度为v甲，由动能定理可得：
m甲gL-μ1m甲g?2L=12m甲v甲2-0，
解得：v甲=

本题解析：

本题难度：一般