微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 太阳质量为M,地球质量为m,地球绕太阳公转的周期为T,万有引力恒量值为G,地球公转半径为R,地球表面重力加速度为g。则以下计算式中正确的是:
A.地球公转所需的向心力为F=mg;
B.地球公转半径 ;
;
C.地球公转的角速度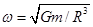 ;
;
D.地球公转的向心加速度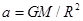 。
。
参考答案:BD
本题解析:地球公转所需的向心力为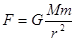 ,r为地日间的距离,A错;由黄金代换
,r为地日间的距离,A错;由黄金代换 可求出地球半径为
可求出地球半径为 ,地球表面的物体受到的万有引力的一个分力提供向心力,并不是完全提供向心力
,地球表面的物体受到的万有引力的一个分力提供向心力,并不是完全提供向心力 不成立,再者不能根据围绕太阳转动的物理量去求地球自转角速度,C错;D对;
不成立,再者不能根据围绕太阳转动的物理量去求地球自转角速度,C错;D对;
本题难度:简单
2、选择题 2013年2月16日凌晨,2012DA14小行星与地球“擦肩而过”,距离地球最近约2.77万公里.据观测,它绕太阳公转的周期约为366天,比地球的公转周期多1天.假设小行星和地球绕太阳运行的轨道均为圆轨道,对应的轨道半径分别为R1、R2,线速度大小分别为v1、v2,以下关系式正确的是( )
A.
=
B.
=
C.
=
D.
=
参考答案:由开普勒行星运行定律R3T2=k有:
R31T21=R32T22?R31R32=T21T22=36623652,故B正确A错误;
万有引力提供圆周运动的向心力
GmMr2=mv2r?v=
本题解析:
本题难度:简单
3、选择题 某同学在研究性学习中记录了一些与地球、月球有关的数据资料如图中表所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中错误的是( )
| 地球半径 | R=6400km
| | 月球半径 | r=1740km
| | 地球表面重力加速度 | g0=9.80m/s2
| | 月球表面重力加速度 | g′=1.56m/s2
| | 月球绕地球转动的线速度 | v=1km/s
| | 月球绕地球转动周期 | T=27.3天
| | 光速 | c=2.998×105 km/s
| 用激光器向月球表面发射激光光束,经过约t=2.565s接收到从月球表面反射回来的激光信号
|
A.s=c?
B.s=-R-r
C.s=-R-r
D.s=-R-r
参考答案:A、由题,激光器发出激光束从发出到接收的时间为t=2.565s,光速为c,则有:s=c?t2.故A正确.
B、由题,月球绕地球转动的线速度为:v=1km/s,周期为:T=27.3s,则月球公转的半径为:R′=vT2π,s=R′-R-r=vT2π-R-r.故B正确.
C、月球表面的重力加速度g′与月球绕地球转动的线速度v没有关系,不能得到g′=v2R′,则不能求出R′=v2g′.故C错误.
D、以月球为研究对象,月球绕地球公转时,由地球的万有引力提供向心力.设地球质量为M,月球的质量为m,则得:GMmR′2=m4π2T2R′,
又在地球表面,有:g0=GMR2
联立上两式得:R′=3g0R2T24π2
本题解析:
本题难度:简单
4、计算题 已知地球半径为R,地球表面重力加速度为g,万有引力常量为G,不考虑地球自转的影响。
(1)求卫星环绕地球运行的第一宇宙速度v1;
(2)若卫星绕地球做匀速圆周运动且运行周期为T,求卫星运行半径r;
(3)由题目所给条件,请提出一种估算地不堪平均密度的方法,并推导出密度表达式。
参考答案:
本题解析:略
本题难度:一般
5、选择题 经国际小行星命名委员会命名的“神舟星”和“杨利伟星”的轨道均处在火星和木星轨道之间,它们绕太阳沿椭圆轨道运行,其轨道参数如下表。
?
| 远日点
| 近日点
| 神舟星
| 3.575AU
| 2.794AU
| 杨利伟星
| 2.197AU
| 1.649AU
|
注:AU是天文学中的长度单位,1AU="149" 597 870 700m(大约是地球到太阳的平均距离)。
“神舟星”和“杨利伟星”绕太阳运行的周期分别为T1和T2,它们在近日点的加速度分别为a1和a2。则下列说法正确的是
A. , , ? B. ? B.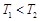 , ,
C. , ,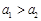 ?D. ?D.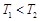 , ,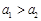
参考答案:A
本题解析:通过表格数据的比较,“神舟星”据太阳的距离比“杨利伟星”更远,也就是“神舟星”轨道的半长轴R更大,据开普勒第三定律:k=R3/T2,“神舟星”的周期较大;又据GM/R2=a可知,两星在近日点的向心加速度比较中,由于“杨利伟星”据太阳的距离较小,所以“杨利伟星”的向心加速度较大,则A选项正确。
本题难度:一般
|
|
|
网站客服QQ: 960335752 - 14613519 - 791315772