1、选择题  下列说法中正确的是（　　）
A．万有引力定律揭示了自然界有质量的物体间普遍存在的一种相互吸引力
B．牛顿发现万有引力定律时，给出了引力常量的值
C．引力常量G的单位是N?kg2/m2
D．两个人站在一起，没有互相靠拢，是因为这时万有引力不存在

参考答案：A

本题解析：

本题难度：简单

2、选择题  为了迎接太空时代的到来，美国国会通过一项计划：在2050年前建造成太空升降机，就是把长绳的一端搁置在地球的卫星上，另一端系住升降机，放开绳，升降机能到达地球上，科学家可以控制卫星上的电动机把升降机拉到卫星上。已知地球表面的重力加速度g=10m/s2，地球半径R＝6400km，地球自转周期为24h。某宇航员在地球表面测得体重为800N，他随升降机垂直地面上升，某时刻升降机加速度为10m/s2，方向竖直向上，这时此人再次测得体重为850N，忽略地球公转的影响，根据以上数据(? )
A．可以求出升降机此时所受万有引力的大小
B．可以求出此时宇航员的动能
C．可以求出升降机此时距地面的高度
D．如果把绳的一端搁置在同步卫星上，可知绳的长度至少有多长

参考答案：CD

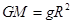本题解析：根据牛顿第二定律：N-mg′=ma，可求出此时的重力加速度g′，升降机此时所受到的万有引力为g′，因为不知道升降机的质量，所以求不出升降机所受的万有引力，故A错误；根据地球表面人的体重和地球表面的重力加速度，可知宇航员质量为80kg，但宇航员此时的速度无法求出，故选项B错误；再根据万有引力等于重力可得：，G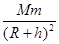=mg′，可求出升降机此时距地面的高度h，故C正确；根据万有引力提供向心力可得：G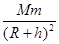=m（R+h），GM=gR2，T=24h，可求出同步卫星离地面的高度，此高度即为绳长的最小值，故D正确．故本题选CD．

本题难度：一般

3、选择题  由于万有引力定律和库仑定律都满足“平方反比定律”，因此引力场和电场之间有许多相似的特性，在处理有关问题时可以将他们进行类比，例如电场中反映各点电场强弱的物理量是电场强度，其定义式为E=F/q，在引力场中可以有一个类似的物理量来反映各点引力场的强弱，设地球的质量为M，半径为R，地球表面处重力加速度为g，引力常量为G，如果一个质量为m的物体位于距地心2R的某点，则下列表达式中能反映该点引力场强弱的是
[? ]
A．
B．
C．
D．g/2

参考答案：A

本题解析：

本题难度：简单

4、选择题  中子星是恒星世界的“侏儒”，其直径一般在20km ～40km ，但其密度大得惊人，若某中子星半径为10km ，密度为1.2 ×1017kg/m3，那么该中子星的卫星环绕速度应为
[? ]
A．约7.9 km/s?
B．约16.7 km/s
C．约3.3 ×102km/s?
D．约5.8 ×104km/s

参考答案：D

本题解析：

本题难度：一般

5、简答题  在地球表面，某物体用弹簧秤竖直悬挂且静止时，弹簧秤的示数为160N，把该物体放在航天器中，若航天器以加速度a=g/2（g为地球表面的重力加速度）竖直上升，在某一时刻，将该物体悬挂在同一弹簧秤上，弹簧秤的示数为90N，若不考虑地球自转的影响，已知地球半径为R=6.4×103km，取g=10m/s2．求：
（1）此时物体所受的重力；
（2）此时航天器距地面的高度．

参考答案：（1）对静止在地球表面的物体进行受力分析，物体受重力和弹簧的拉力F．
? G0=mg=F=160N．
其中g为地球表面的重力加速度，取10m/s2
则得出物体质量m=16Kg．
该物体放在航天器中，对物体进行受力分析，物体受重力和弹簧的拉力T．
航天器中以a=g2的加速度匀加速竖直向上，根据牛顿第二定律得：
? T-G′=ma
由题T=90N，代入解得：G′=10N．
（2）由于不考虑地球自转的影响，根据万有引力等于重力得出：
在地球表面：G0=GMmR2
在航天器中：G′=GMmr2
则R2r2=G′G=10160
所以r=4R=4×6.4×103km
即此时航天器距地高度为h=r-R=3R=3×6.4×103km=1.92×104Kkm．
答：（1）此时物体所受的重力为10N；
（2）此时航天器距地面的高度是1.92×104Kkm．

本题解析：

本题难度：一般