微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
; 根据准则1,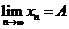 存在
存在
在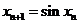 两边取极限得
两边取极限得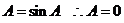
因此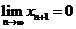
(2)原式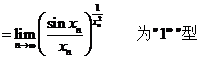
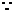 离散型不能直接用洛必达法则
离散型不能直接用洛必达法则
先考虑 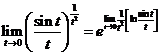
用洛必达法则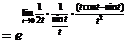
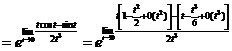
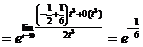 .
.
(19)证明:当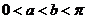 时,
时,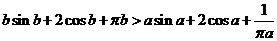 .
.
证:令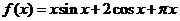
只需证明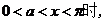
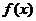 严格单调增加
严格单调增加
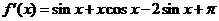
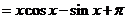
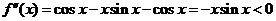
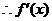 严格单调减少
严格单调减少
又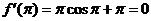
故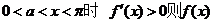 单调增加(严格)
单调增加(严格)
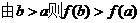 得证
得证
(20)设函数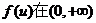 内具有二阶导数,且
内具有二阶导数,且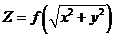 满足等式
满足等式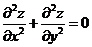 .
.
(I)验证 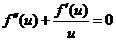 ;
;
(II)若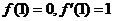 求函数
求函数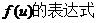 .
.
证:(I)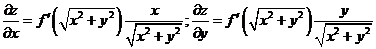
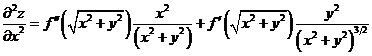
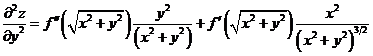
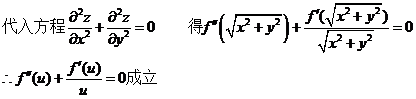
(II)令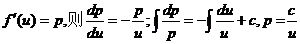
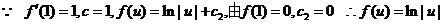
(21)已知曲线L的方程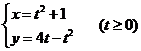
(I)讨论L的凹凸性;
(II)过点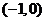 引L的切线,求切点
引L的切线,求切点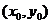 ,并写出切线的方程;
,并写出切线的方程;
(III)求此切线与L(对应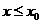 部分)及x轴所围的平面图形的面积.
部分)及x轴所围的平面图形的面积.
解:(I)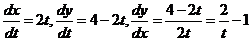
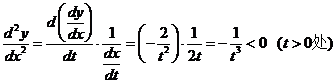
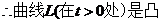
(II)切线方程为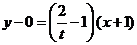 ,设
,设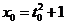 ,
,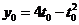 ,
,
则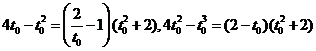
得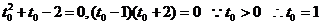
点为(2,3),切线方程为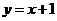
(III)设L的方程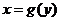
则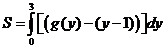
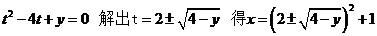
由于(2,3)在L上,由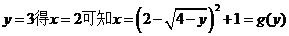
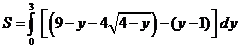
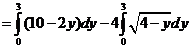
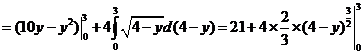
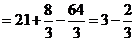
(22)已知非齐次线性方程组
 x1+x2+x3+x4=-1,
x1+x2+x3+x4=-1,
4x1+3x2+5x3-x4=-1,
ax1+x2+3x3+bx4=1
有3个线性无关的解.
① 证明此方程组的系数矩阵A的秩为2.
② 求a,b的值和方程组的通解.
解:① 设a1,a2,a3是方程组的3个线性无关的解,则a2-a1,a3-a1是AX=0的两个线性无关的解.于是AX=0的基础解系中解的个数不少于2,即4-r(A)³2,从而r(A)£2.
又因为A的行向量是两两线性无关的,所以r(A)³2.
两个不等式说明r(A)=2.
② 对方程组的增广矩阵作初等行变换:



 1 1 1 1 -1 1 1 1 1 -1
1 1 1 1 -1 1 1 1 1 -1
(A|b)= 4 3 5 -1 -1 ® 0 –1 1 –5 3 ,
a 1 3 b 1 0 0 4-2a 4a+b-5 4-2a
由r(A)=2,得出a=2,b=-3.代入后继续作初等行变换:

 1 0 2 -4 2
1 0 2 -4 2
® 0 1 -1 5 -3 .
0 0 0 0 0
得同解方程组
 x1=2-2x3+4x4,
x1=2-2x3+4x4,
x2=-3+x3-5x4,
求出一个特解(2,-3,0,0)T和AX=0的基础解系(-2,1,1,0)T,(4,-5,0,1) T.得到方程组的通解: (2,-3,0,0)T+c1(-2,1,1,0)T+c2(4,-5,0,1)T, c1,c2任意.
(23) 设3阶实对称矩阵A的各行元素之和都为3,向量a1=(-1,2,-1)T, a2=(0,-1,1)T都是齐次线性方程组AX=0的解.
① 求A的特征值和特征向量.
② 求作正交矩阵Q和对角矩阵L,使得 Q TAQ=L.
解:① 条件说明A(1,1,1)T=(3,3,3)T,即 a0=(1,1,1)T是A的特征向量,特征值为3.又a1,a2都是AX=0的解说明它们也都是A的特征向量,特征值为0.由于a1,a2线性无关, 特征值0的重数大于1.于是A的特征值为3,0,0.
属于3的特征向量:ca0, c¹0.
属于0的特征向量:c1a1+c2a2, c1,c2不都为0.
② 将a0单位化,得h0=(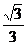 ,
,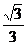 ,
,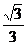 )T.
)T.
对a1,a2作施密特正交化,的h1=(0,-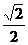 ,
,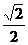 )T, h2=(-
)T, h2=(-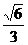 ,
,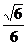 ,
,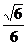 )T.
)T.
作Q=(h0,h1,h2),则Q是正交矩阵,并且
 3 0 0
3 0 0
Q TAQ=Q-1AQ= 0 0 0 .
0 0 0