微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
]
【分析】 先两两进行比较,再排出次序即可.
【详解】 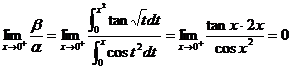 ,可排除(C),(D)选项,
,可排除(C),(D)选项,
又 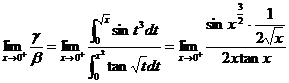
=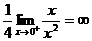 ,可见
,可见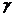 是比
是比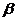 低阶的无穷小量,故应选(B).
低阶的无穷小量,故应选(B).
【评注】 本题是无穷小量的比较问题,也可先将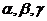 分别与
分别与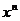 进行比较,再确定相互的高低次序.
进行比较,再确定相互的高低次序.
完全类似例题见《数学一临考演习》P28第9题.
(8)设函数f(x)连续,且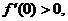 则存在
则存在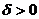 ,使得
,使得
(A) f(x)在(0,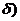 内单调增加. (B)f(x)在
内单调增加. (B)f(x)在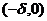 内单调减少.
内单调减少.
(C) 对任意的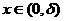 有f(x)>f(0) . (D) 对任意的
有f(x)>f(0) . (D) 对任意的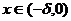 有f(x)>f(0) . [ C ]
有f(x)>f(0) . [ C ]
【分析】 函数f(x)只在一点的导数大于零,一般不能推导出单调性,因此可排除(A),(B)选项,再利用导数的定义及极限的保号性进行分析即可。
【详解】 由导数的定义,知
 ,
,
根据保号性,知存在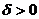 ,当
,当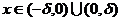 时,有
时,有
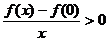
即当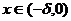 时,f(x)<f(0); 而当
时,f(x)<f(0); 而当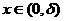 时,有f(x)>f(0). 故应选(C).
时,有f(x)>f(0). 故应选(C).
【评注】 题设函数一点可导,一般均应联想到用导数的定义进行讨论。
完全类似例题见《数学一临考演习》P28第10题.
(9)设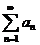 为正项级数,下列结论中正确的是
为正项级数,下列结论中正确的是
(A) 若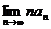 =0,则级数
=0,则级数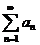 收敛.
收敛.
(B) 若存在非零常数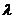 ,使得
,使得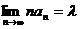 ,则级数
,则级数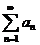 发散.
发散.
(C) 若级数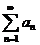 收敛,则
收敛,则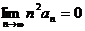 .
.
(D) 若级数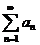 发散, 则存在非零常数
发散, 则存在非零常数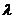 ,使得
,使得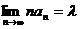 . [ B ]
. [ B ]
【分析】 对于敛散性的判定问题,若不便直接推证,往往可用反例通过排除法找到正确选项.
【详解】 取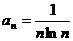 ,则
,则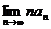 =0,但
=0,但 发散,排除(A),(D);
发散,排除(A),(D);
又取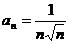 ,则级数
,则级数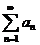 收敛,但
收敛,但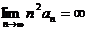 ,排除(C), 故应选(B).
,排除(C), 故应选(B).
【评注】 本题也可用比较判别法的极限形式,
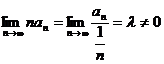 ,而级数
,而级数 发散,因此级数
发散,因此级数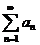 也发散,故应选(B).
也发散,故应选(B).
完全类似的例题见《数学复习指南》P213例8.13.
(10)设f(x)为连续函数,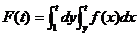 ,则
,则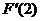 等于
等于
(A) 2f(2). (B) f(2). (C) –f(2). (D) 0. [ B ]
【分析】 先求导,再代入t=2求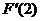 即可。关键是求导前应先交换积分次序,使得被积函数中不含有变量t.
即可。关键是求导前应先交换积分次序,使得被积函数中不含有变量t.
【详解】 交换积分次序,得
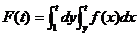 =
=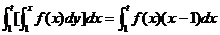
于是, ,从而有
,从而有 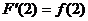 ,故应选(B).
,故应选(B).
【评注】 在应用变限的积分对变量x求导时,应注意被积函数中不能含有变量x:

否则,应先通过恒等变形、变量代换和交换积分次序等将被积函数中的变量x换到积分号外或积分线上。
完全类似例题见《数学最后冲刺》P184例12,先交换积分次序再求导.
(11)设A是3阶方阵,将A的第1列与第2列交换得B,再把B的第2列加到第3列得C, 则满足AQ=C的可逆矩阵Q为
(A)  . (B)
. (B) 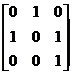 . (C)
. (C)  . (D)
. (D)  .
.
[ D ]
【分析】 本题考查初等矩阵的的概念与性质,对A作两次初等列变换,相当于右乘两个相应的初等矩阵,而Q即为此两个初等矩阵的乘积。
【详解】由题设,有
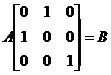 ,
, 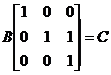 ,
,
于是, 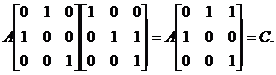
可见,应选(D).
【评注】 涉及到初等变换的问题,应掌握初等矩阵的定义、初等矩阵的性质以及与初等变换的关系。
完全类似例题见《数学题型集粹与练习题集》P196例2.2
(12)设A,B为满足AB=O的任意两个非零矩阵,则必有
(A) A的列向量组线性相关,B的行向量组线性相关.
(B) A的列向量组线性相关,B的列向量组线性相关.
(C) A的行向量组线性相关,B的行向量组线性相关.
(D) A的行向量组线性相关,B的列向量组线性相关. [ A ]
【分析】A,B的行列向量组是否线性相关,可从A,B是否行(或列)满秩或Ax=0(Bx=0)是否有非零解进行分析讨论.
【详解1】 设A为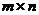 矩阵,B 为
矩阵,B 为 矩阵,则由AB=O知,
矩阵,则由AB=O知,
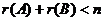 .
.
又A,B为非零矩阵,必有r(A)>0,r(B)>0. 可见r(A)<n, r(B)<n, 即A的列向量组线性相关,B的行向量组线性相关,故应选(A).
【详解2】 由AB=O知,B的每一列均为Ax=0的解,而B为非零矩阵,即Ax=0存在非零解,可见A的列向量组线性相关。
同理,由AB=O知, ,于是有
,于是有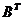 的列向量组,从而B的行向量组线性相关,故应选(A).
的列向量组,从而B的行向量组线性相关,故应选(A).
【评注】 AB=O是常考关系式,一般来说,与此相关的两个结论是应记住的:
1) AB=O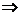
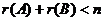 ;
;
2) AB=O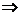 B的每列均为Ax=0的解。
B的每列均为Ax=0的解。
完全类似例题见《数学最后冲刺》P110例10-11,《数学一临考演习》P79第4题,〈考研数学大串讲〉P173例8, P184例27。
(13)设随机变量X服从正态分布N(0,1),对给定的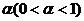 ,数
,数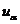 满足
满足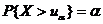 ,若
,若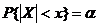 ,则
,则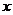 等于
等于
(A) 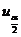 . (B)
. (B)  . (C)
. (C) 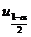 . (D)
. (D) 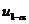 . [ C ]
. [ C ]
【分析】 此类问题的求解,可通过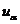 的定义进行分析,也可通过画出草图,直观地得到结论。
的定义进行分析,也可通过画出草图,直观地得到结论。
【详解】 由标准正态分布概率密度函数的对称性知, ,于是
,于是
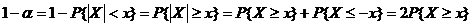
即有 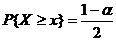 ,可见根据定义有
,可见根据定义有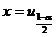 ,故应选(C).
,故应选(C).
 【评注】 本题
【评注】 本题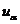 相当于分位数,直观地有
相当于分位数,直观地有



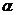
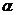
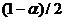


 o
o 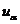
此类问题在文登学校的辅导班上作为正态分布的一般结论总结过.
(14)设随机变量 独立同分布,且其方差为
独立同分布,且其方差为 令
令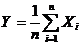 ,则
,则
(A) Cov( (B)
(B) 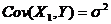 .
.
(C) 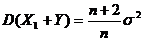 . (D)
. (D) 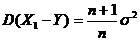 . [ A ]
. [ A ]
【分析】 本题用方差和协方差的运算性质直接计算即可,注意利用独立性有: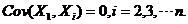
【详解】 Cov(
&n