微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
自变量求偏导数(或导数),此时一定要注意谁是自变量,谁是因变量,对中间变量的求导不要漏项。然后求解相应的线性方程式或方程组,求得所要的隐函数的偏导数或导数。
2. 利用一阶全微分形式的不变性,对每个方程两边求全微分,此时各变量的地位是平等的,然后求解相应的线性方程组或者方程式,求的相应的隐函数的全微分。
对于多元隐函数来说,若题目中求的是全部偏导数或全微分,往往是用方法2比较简单些,若只求某个偏导数,则方法1和方法2的繁简程度差不多。
在本题中,
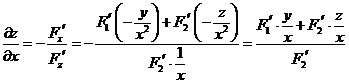 ,
,
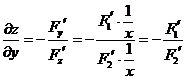 ,
,
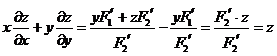
(3) 设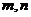 是正整数,则反常积分
是正整数,则反常积分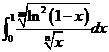 的收敛性 ( )
的收敛性 ( )
(A) 仅与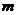 的取值有关. (B) 仅与
的取值有关. (B) 仅与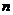 的取值有关.
的取值有关.
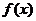 (C) 与
(C) 与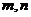 的取值都有关. (D) 与
的取值都有关. (D) 与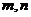 的取值都无关.
的取值都无关.
【答案】D
【考点】反常积分
【详解】本题涉及到的主要知识点:
反常积分敛散性判别法则:设f(x)在(a,b)非负,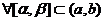 ,
,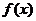 在
在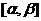 可积,又设
可积,又设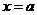 (或
(或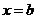 )是
)是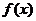 的瑕点,且
的瑕点,且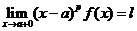 (或
(或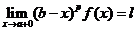 ),则当
),则当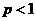 且
且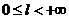 时瑕积分
时瑕积分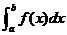 收敛。
收敛。
在本题中,
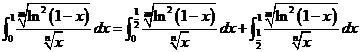 ,
,
对于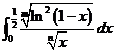 ,瑕点为
,瑕点为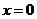
设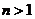 ,
,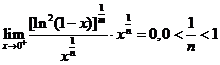 故收敛。
故收敛。
设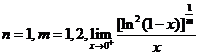 存在,
存在,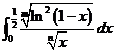 不是反常积分
不是反常积分
设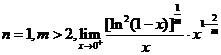 存在,
存在,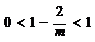 ,故
,故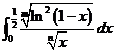 收敛。
收敛。
对于,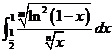 ,瑕点为
,瑕点为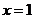 ,当
,当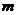 为正整数时,
为正整数时,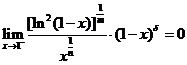 ,其中
,其中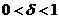 ,故
,故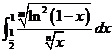 收敛
收敛
故选(D)。
(4) 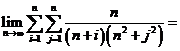 ( )
( )
(A) 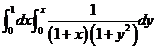 . (B)
. (B) 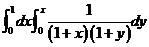 .
.
(C) 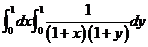 . (D)
. (D) 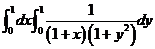 .
.
【答案】D
【考点】定积分的概念
【详解】本题涉及到的主要知识点:
利用定积分的定义求某些n项和式的极限(先将和式表示成某函数在某区间上的一个积分和,它的极限就是一个定积分)。
特别是对于n项和数列的极限,应该注意到:
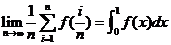
其中多几项或少几项并不影响结果。
在本题中,
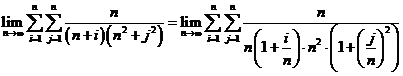
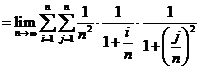
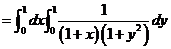
(5) 设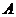 为
为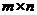 型矩阵,
型矩阵,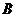 为
为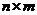 型矩阵,
型矩阵,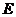 为
为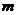 阶单位矩阵,若
阶单位矩阵,若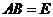 ,则 ( )
,则 ( )
(A) 秩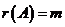 ,秩
,秩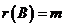 . (B) 秩
. (B) 秩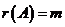 ,秩
,秩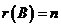 .
.
(C) 秩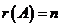 ,秩
,秩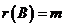 . (D) 秩
. (D) 秩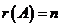 ,秩
,秩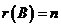 .
.
【答案】A
【考点】矩阵的秩
【详解】本题涉及到的主要知识点:
矩阵的秩的定义,若一个矩阵A的行向量组的秩和列向量组的秩相等,称此数为矩阵A的秩。记做r(A)。若r(A)=r,则A中有r阶子式不为0,而r+1阶子式必全为0.
矩阵秩的重要公式:
1)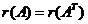
2)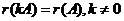
3)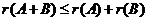
4)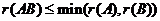
5)若A可逆,则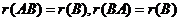
6)若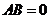 ,
,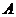 是
是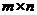 矩阵,则
矩阵,则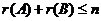
7)若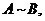 则
则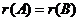
在本题中,
由于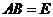 ,故
,故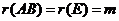 .又由于
.又由于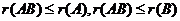 ,故
,故
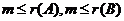 ①
①
由于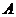 为
为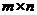 矩阵,
矩阵,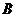 为
为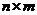 矩阵,故
矩阵,故
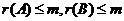 ②
②
由①、②可得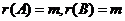 ,故选A.
,故选A.
(6) 设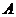 为4阶实对称矩阵,且
为4阶实对称矩阵,且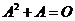 ,若
,若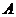 的秩为3,则
的秩为3,则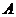 相似于 ( )
相似于 ( )
(A)  . (B)
. (B) 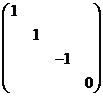 .
.
(C)  . (D)
. (D) 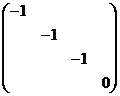 .
.
【答案】D
【考点】矩阵的特征值和特征向量;相似对角矩阵
【详解】本题涉及到的主要知识点:
(i)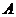 与对角矩阵相似的充分条件:①
与对角矩阵相似的充分条件:①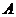 有
有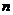 个不同的特征值;②
个不同的特征值;②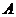 是实对称矩阵
是实对称矩阵
(ii)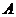 与对角矩阵相似的充要条件:对于矩阵
与对角矩阵相似的充要条件:对于矩阵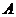 的每一个
的每一个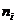 重特征值
重特征值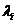 ,其线性无关的特征向量的个数恰好等于该特征值的重根数
,其线性无关的特征向量的个数恰好等于该特征值的重根数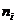 ,即秩
,即秩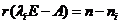 .
.
在本题中,
设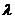 为
为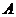 的特征值,由于
的特征值,由于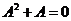 ,所以
,所以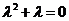 ,即
,即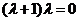 ,这样
,这样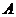 的特征值为-1或0.由于
的特征值为-1或0.由于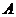 为实对称矩阵,故
为实对称矩阵,故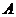 可相似对角化,即
可相似对角化,即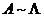 ,
,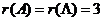 ,因此,
,因此, ,即
,即 .
.
(7) 设随机变量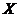 的分布函数
的分布函数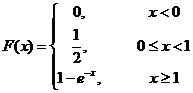 ,则
,则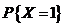 = ( )
= ( )
(A) 0. (B) 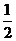 . (C)
. (C) 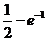 . (D)
. (D) 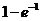 .
.
【答案】C
【考点】随机变量分布函数的概念及其性质
【详解】本题涉及到的主要知识点:
(i)设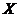 是一个随机变量,
是一个随机变量,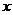 是任意实数,函数
是任意实数,函数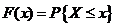 ,
,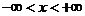
称为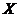 的分布函数.
的分布函数.
(ii)设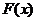 是随机变量
是随机变量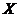 的分布函数,则对任意两个实数
的分布函数,则对任意两个实数 ,有
,有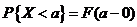 .
.
在本题中,
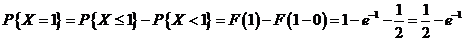
(8) 设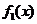 为标准正态分布的概率密度,
为标准正态分布的概率密度,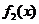 为
为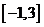 上均匀分布的概率密度,若
上均匀分布的概率密度,若
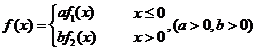
为概率密度,则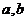 应满足 ( )
应满足 ( )
(A) 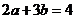 . (B)
. (B)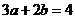 . (C)
. (C) . (D)
. (D)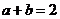 .
.
【答案】A
【考点】常见随机变量的分布;二维连续型随机变量的概率密度
【详解】本题涉及到的主要知识点:
(i)标准正态分布概率密度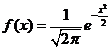 ,
,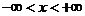
(ii)均匀分布概率密度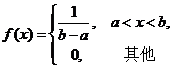
(iii)概率密度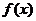 具有的性质:
具有的性质: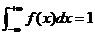
在本题中,
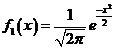 ,
,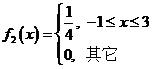
利用概率密度的性质
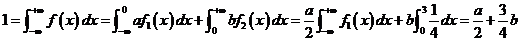
所以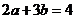 .
.
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9) 设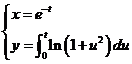 ,求
,求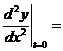
 .
.
【答案】0
【考点】参数方程所确定的函数的微分法
【详解】本题涉及到的主要知识点:
由参数方程确定函数的运算法则:
设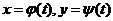 确定函数
确定函数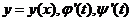 存在
存在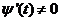 ,则
,则
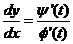
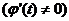
二阶导数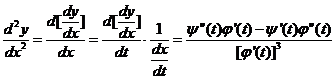
在本题中,
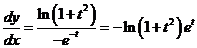 ,
,
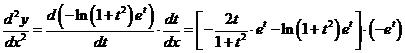 ,
, 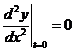
(10) 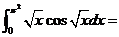
 .
.
【答案】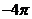
【考点】定积分的换元法和分部积分法
【详解】本题涉及到的主要知识点:
第一换元积分法
设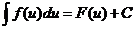 ,又
,又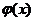 可导,则
可导,则
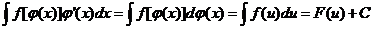
第二类换元积分法:
设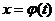 可导,且
可导,且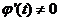 ,若
,若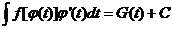 ,
,
则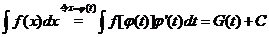 ,其中
,其中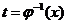 为
为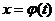 的反函数。
的反函数。
分部积分法:
设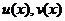 均有连续的导数,则
均有连续的导数,则
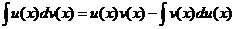 或者
或者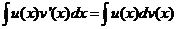
在本题中,
令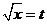 ,
,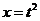 ,
,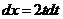
原式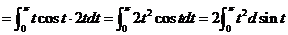
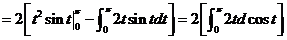
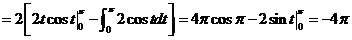
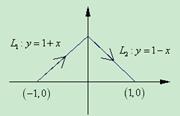
(11) 已知曲线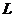 的方程为
的方程为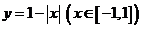 ,起点是
,起点是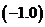 ,终点是
,终点是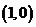 ,则曲线积分
,则曲线积分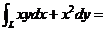
 .
.
【答案】0
【考点】第二类曲线积分
【详解】本题涉及到的主要知识点:
曲线积分的基本计算方法是:代公式,化为定积分,特别要注意定积分限的配置,第二类线积分与曲线定向有关,第一类曲线积分与曲线定向无关。
在本题中,
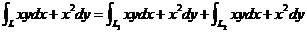
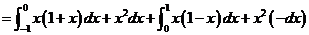
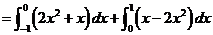
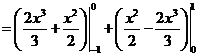
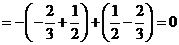
(12) 设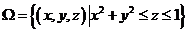 ,则
,则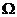 的形心的竖坐标
的形心的竖坐标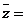
 .
.
【答案】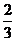
【考点】曲线积分和曲面积分的应用
【详解】本题涉及到的主要知识点:
多元函数积分学的应用包括几何应用(求平面图形与曲面的面积、求空间立体的体积与空间曲线的弧长)与物理应用(求变力做功,物体的重心,转动惯量,引力及流体的流量等)。
三重积分的应用主要有两种情形:
(1)截面面积已知的情形
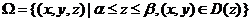 ,
,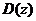 的面积为S(z),则
的面积为S(z),则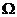 的体积
的体积
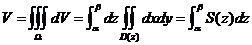
(2)曲顶面底柱形区域的情形。
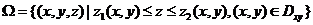 ,
,
则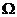 的体积
的体积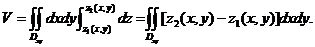
在这种情形要确定上、下曲面及投影区域。
在本题中,
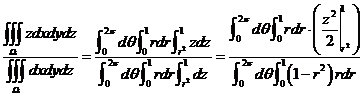
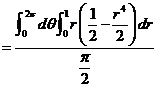
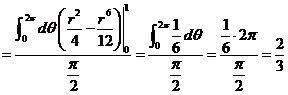
(13) 设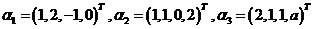 ,若由
,若由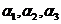 形成的向量空间
形成的向量空间
维数是2,则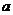 =
= .
.
【答案】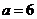
【考点】向量空间维数的概念
【详解】本题涉及到的主要知识点:
向量空间这部分的内容应当了解向量空间、子空间、维数等概念,然后利用向量组秩的有关定义求得未知数。
在本题中,
因为由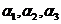 形成的向量空间维数为2,所以
形成的向量空间维数为2,所以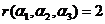 .对
.对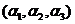 进行初等行变换:
进行初等行变换:
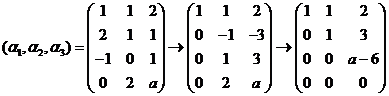
所以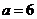 .
.
(14) 设随机变量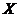 的概率分布为
的概率分布为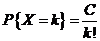 ,
,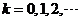 ,则
,则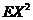 =
=  .
.
【答案】2