1、选择题  某人在地面上用弹簧秤称得体重为490N。他将弹簧秤移至电梯内称其体重，t0至t3时间段内，弹簧秤的示数如图所示，电梯运行的v-t图可能是（取电梯向上运动的方向为正）

[? ]
A.
B.
C.
D.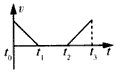

参考答案：A

本题解析：

本题难度：一般

2、简答题  摩天大楼中一部直通高层的客运电梯．行程超过百米．电梯的简化模型如下所示．电梯的加速度a随时间t变化的．已知电梯在t=0时由静止开始上升，a一t图象如图2所示．电梯总质最m=2.0x103kg．忽略一切阻力．重力加速度g取10m/s2．求
（1）电梯在上升过程中受到的最大拉力F1和最小拉力F2；
（2）类比是一种常用的研究方法．对于直线运动，教科书中讲解了由v-t图象求位移的方法．请你借鉴此方法，对比加速度的和速度的定义，根据图2所示a-t图象，求电梯在第1s内的速度改变量△v1和第2s末的速率v2；
（3）电梯以最大速率上升时，拉力做功的功率p；
（4）求在0～11s时间内，拉力和重力对电梯所做的总功w．

参考答案：解；（1）由牛顿第二定律，有?F-mg=ma
由a─t图象可知，F1和F2对应的加速度分别是a1=1.0m/s2，a2=-1.0m/s2
则
? F1=m（g+a1）=2.0×103×（10+1.0）N=2.2×104N
? F2=m（g+a2）=2.0×103×（10-1.0）N=1.8×104N
（2）通过类比可得，电梯的速度变化量等于第1s内a─t图线下的面积
△υ1=0.50m/s
同理可得，△υ2=υ2-υ0=1.5m/s
υ0=0，第2s末的速率υ2=1.5m/s
（3）由a─t图象可知，11s～30s内速率最大，其值等于0～11s内a─t图线下的面积，有
? υm=10m/s
此时电梯做匀速运动，拉力F等于重力mg，所求功率
P=Fυm=mg?υm=2.0×103×10×10W=2.0×105W
（4）由动能定理，总功
W=Ek2-Ek1=12mυm2-0=12×2.0×103×102J=1.0×105J
答：
（1）电梯在上升过程中受到的最大拉力F1是2.2×104N，最小拉力F2是1.8×104N．
（2）电梯在第1s内的速度改变量△υ1是0.50m/s，第2s末的速率υ2是1.5m/s．
（3）电梯以最大速率上升时，拉力做功的功率P为2.0×105W；
（4）在0─11s时间内，拉力和重力对电梯所做的总功W是1.0×105J．

本题解析：

本题难度：一般

3、计算题  目前我国动车组在广泛使用。假设动车轨道为直线，动车制动时的阻力为重力的0.1倍。（g=10m/s2）
（1）如果动车司机发现前方450m处有故障车停车，要使动车不发生追尾，则动车运行速度不能超过多少？（不考虑反应时间）
（2）如果动车运行的速度为252km/h，当动车司机前方2464m处有故障车停车，经反应后制动减速，为了确保列车不发生追尾，问动车司机反应时间不得超过多少？

参考答案：（1）30m/s?（2）0.2s

本题解析：（1）动车所受阻力
减速的加速度
由，可得?
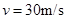（2）
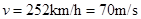
设反应时间为t，反应时间内位移为，减速位移为
?
?
?
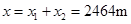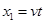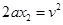可得?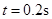
点评：灵活的应用匀变速直线运动的规律是接答本题的关键。

本题难度：简单

4、选择题  在升降机内，一个人站在台秤上，当升降机运动时，此人发现台秤的示数是自身重力的1.2倍，则升降机的运动可能是（?）
A．以0.2g的加速度减速下降
B．以0.2g的加速度加速上升
C．以1.2g的加速度减速下降
D．以1.2g的加速度加速上升

参考答案：AB

本题解析：该同学处于超重状态，加速度向上，所以升降机加速上升或者减速下降，根据N-mg=ma，所以a=0.2g，故升降机以0.2g的加速度加速上升，或者升降机以0.2g的加速度减速下降，AB正确
点评：难度较小，明确加速度方向，能想到加速和减速两种情况是本题所要考查的

本题难度：简单

5、选择题  一斜面固定在水平面上，在斜面顶端有一长木板，木板与斜面之间的动摩擦因数为?，木板上固定一轻质弹簧测力计，弹簧测力计下面连接一个光滑的小球，如图所示，当木板固定时，弹簧测力计示数为 F1，现由静止释放后，木板沿斜面下滑， 稳定时弹簧测力计的示数为 F2，若斜面的高为h，底边长为 d，则下列说法正确的是

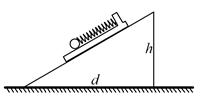
A．稳定后弹簧仍处于伸长状态
B．稳定后弹簧一定处于压缩状态
C．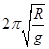
D．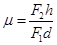

参考答案：AD

本题解析：平衡时，对小球分析F1=mgsinθ；木板运动后稳定时，对整体分析有：a=gsinθ-μgcosθ；则a＜gsinθ，根据牛顿第二定律得知，弹簧对小球的弹力应沿斜面向上，弹簧处于拉伸状态．对小球有mgsinθ-F2=ma而tanθ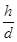＝；联立以上各式计算可得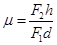．故AD正确．

本题难度：一般