1、计算题 如图所示,水平地面上静止放置一辆小车A,质量mA=4kg,车长l=0.4m,上表面不光滑,小车与地面间的摩擦力极小,可以忽略不计。小车以v=1.2m/s在水平地面匀速运动。将可视为质点的物块B无初速度地置于A的最右端,B的质量mB=2kg,A、B间的动摩擦因素为μ=0.2,AB间的最大静摩擦力可以认为等于滑动摩擦力。现对A施加一个水平向右的恒力F作用。(g=10m/s2,所有计算结果保留两位有效数字)
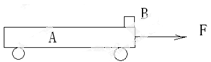
(1).要维持小车匀速运动,求F的大小?
(2).当A匀速运动时,求从B放上A至B相对A静止,A发生的位移大小?
(3)要使物块B不从小车A上掉下,求F的大小?
参考答案:(1)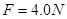 或者
或者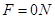 (2)
(2)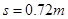 (3)
(3)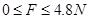
本题解析:(1)A相对B向右运动,A受到B对它的向左的滑动摩擦力,大小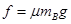
要维持A的匀速运动,由平衡条件可知,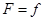 ,解得
,解得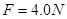
当B与A的速度相同时,要维持A的匀速运动,对AB整体,由平衡条件可得,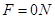
(2)B在滑动摩擦力作用下做匀加速运动,加速到大小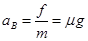
从B放上A到B相对A静止,B运动时间为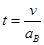
在t时间内,A发生的位移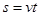 ,解得
,解得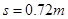
(3)当外力F到达最大时,A加速,B加速,且B滑至A的最左端,AB同速,
对A: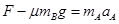
当AB同速时,经历的时间为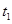 ,则
,则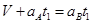
在时间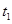 内,A发生的位移
内,A发生的位移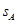 ,B发生的位移
,B发生的位移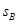 ,
,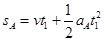 ,
,
且位移满足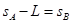 ,解得
,解得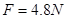 ,AB共同运动的加速度
,AB共同运动的加速度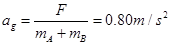
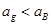 ,到达共速后,AB以
,到达共速后,AB以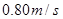 做匀速运动,A不会滑离B
做匀速运动,A不会滑离B
F越小,B在A上的相对位移越小,所以要使B不从A上滑落,F的取值范围是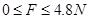
考点:考查了牛顿第二定律,运动学公式的综合应用
本题难度:一般
2、计算题 如图所示,光滑水平面上固定一倾斜角为30o的光滑斜面,紧靠斜面底端有一质量为4kg的木板,木板与斜面底端之间通过微小弧形轨道相接,以保证滑块从斜面滑到木板的速度大小不变。质量为2kg的滑块从斜面上高h=1.8m处由静止滑下,并以到达倾斜底端的速度滑上木板左端,最终滑块没有从木板上滑下。已知滑块与木板间的动摩擦因数μ=0.2,取g=10m/s2求:(1)滑块从滑上木板到与木板速度相同经历的时间(2)木板的最短长度;
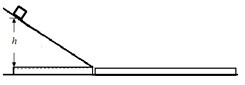
参考答案:(1)2s (2)6m
本题解析:(1)木块下滑的加速度:a=gsin300
滑到低端的速度:
解得:v=6m/s.
物块在木板上滑动的加速度:a1=μg=2m/s2
木板的加速度: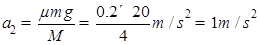
两者共速时:v共=v-a1t=a2t ,解得:t=2s v共=2m/s
(2)共速时木块的位移: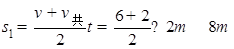
木板的位移:
木板的最小长度:L=s1-s2=6m
考点:牛顿第二定律的应用.
本题难度:一般
3、计算题 如图所示,光滑水平面上固定一倾斜角为37?的粗糙斜面,紧靠斜面底端有一质量为4kg的木板,木板与斜面底端之间通过微小弧形轨道相接,以保证滑块从斜面滑到木板的速度大小不变。质量为2kg的滑块从斜面上高h=5m处由静止滑下,到达倾斜底端的速度为v0=6m/s,并以此速度滑上木板左端,最终滑块没有从木板上滑下。已知滑块与木板间的动摩擦因数μ2=0.2,取g=10m/s2,sin370=0.6,cos370=0.8。求:
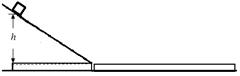
(1)斜面与滑块间的动摩擦因数μ1;
(2)滑块从滑上木板到与木板速度相同经历的时间;
(3)木板的最短长度。
参考答案:(1)0.48;(2)2s; (3)6m.
本题解析:(1)在斜面上,由动能定理得: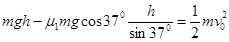
得μ1=0.48
(2)在木板上滑动过程中,有 Ff=μ2mg
由牛顿第二定律得滑块的加速度 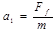 =μ2g= 2m/s
=μ2g= 2m/s
木板的加速度 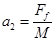 =1m/s2
=1m/s2
由运动学公式 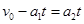
得t=2s
此时v1=v2=2m/s
(3)设木板最短长度为△x,则:x M=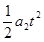
x m=v0t—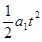
得△x= x m—x M =6m
考点:动能定理及牛顿第二定律。
本题难度:困难
4、计算题 (10分)如图所示,粘有小泥块的小球用长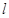 的细绳系于悬点O,小球静止时距水平地面的高度为h。现将小球向左拉偏一角度
的细绳系于悬点O,小球静止时距水平地面的高度为h。现将小球向左拉偏一角度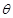 ,使其从静止开始运动。当小球运动到最低点时,泥块恰好从小球上脱落。已知小球质量为M,泥块质量为m,且小球和泥块均可视为质点。求:
,使其从静止开始运动。当小球运动到最低点时,泥块恰好从小球上脱落。已知小球质量为M,泥块质量为m,且小球和泥块均可视为质点。求:
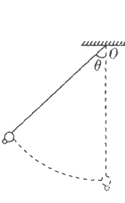
(1)小球运动到最低点泥块刚要脱落时,小球和泥块运动的速度大小;
(2)泥块脱落至落地在空中飞行的水平距离s;
(3)泥块脱离小球后的瞬间小球受到绳的拉力为多大?
参考答案:(1)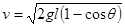 (2)
(2)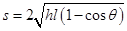 (3)
(3)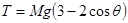
本题解析:(1)小球和泥块下摆过程中,绳的拉力不做功,只有重力做功,所以机械能守恒
因此有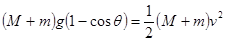 (2分)
(2分)
解得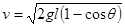 (1分)
(1分)
(2)泥块从小球上脱落后以速度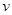 做平抛运动。
做平抛运动。
设泥块的飞行时间为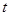 ,则有:
,则有: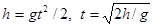 (2分)
(2分)
所以泥块飞行的水平距离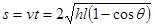 (2分)
(2分)
(3)泥块脱离小球后瞬间,小球在竖直方向受到绳的拉力T和重力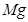 作用,根据牛顿第二定律,有:
作用,根据牛顿第二定律,有: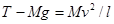 (2分)
(2分)
解得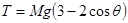 (1分)
(1分)
考点:机械能守恒,平抛运动
本题难度:一般
5、计算题 如图所示,质量为l kg的小球穿在固定的直杆上,杆与水平方向成30°角,球与杆间的动摩擦因数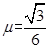 ,当小球受到的竖直向上的拉力F =20N时,试求:
,当小球受到的竖直向上的拉力F =20N时,试求:
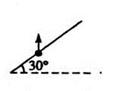
(1)杆给球的弹力的大小和方向?
(2)小球沿杆上滑的加速度是多少?(g=10m/s2)?
参考答案:(1)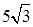 N(2)2.5m/s2
N(2)2.5m/s2
本题解析:(1)小球受力如图,
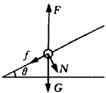
在垂直于杆子方向上合力等于零,有:
N=(F?mg)cos30°=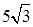 N.
N.
(2) 根据正交分解得,物体所受的合力在沿杆子方向上.F合=(F-mg)sin30°-μ(F-mg)cos30°=2.5N
根据牛顿第二定律得, ,方向沿杆子向上.
,方向沿杆子向上.
考点:牛顿第二定律;正交分解法.
本题难度:一般