|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
中国最大的高考网站,您身边的高考专家。 width=54 height=26 src="/ewebeditor/uploadfile/2015/06/13/20150613134604983121.gif">得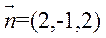 . .
从而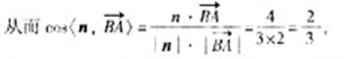
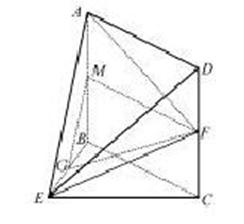 所以平面AEF与平面BEC所成锐二面角的余弦值为 所以平面AEF与平面BEC所成锐二面角的余弦值为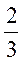 . .
解法二:(1)如图,取AB中点M,连接MG,MF,
又G是BE的中点,可知GM//AE,
又AE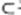 平面ADE,GM¢平面ADE, 平面ADE,GM¢平面ADE,
所以GM//平面ADE.
在矩形ABCD中,由M,F分别是AB,CD的中点得MF//AD.
又AD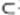 平面ADE,MF¢平面ADE. 平面ADE,MF¢平面ADE.
所以MF//平面ADE.
又因为GM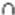 MF=M,GM MF=M,GM 平面GMF.MFC平面GMF. 平面GMF.MFC平面GMF.
所以平面GMF//平面ADF,
因为GF 平面GMF,所以GF//平面ADE 平面GMF,所以GF//平面ADE
(2)同解法一.
18.本小题主要考查椭圆、圆、直线与椭圆的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想. 满分13分
解法一:(1)由已知得

所以椭圆E的方程为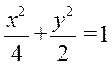 . .
(2)设点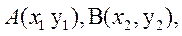 AB中点为 AB中点为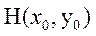 . .
由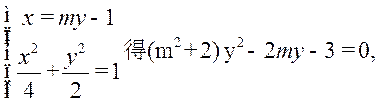
所以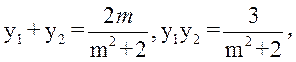 从而 从而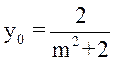 . .
所以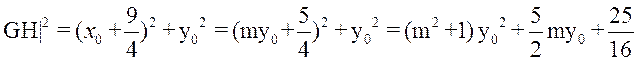 . .
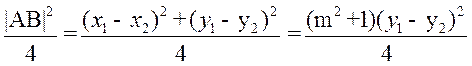
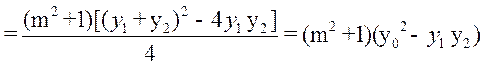 , ,
故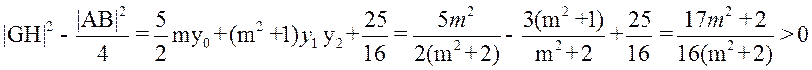
所以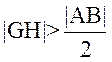 ,故G ,故G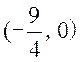 在以AB为直径的圆外. 在以AB为直径的圆外.
解法二:(1)同解法一.
(2)设点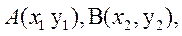 ,则 ,则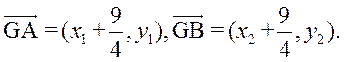
由![]()
|