1、简答题  跳水运动是我国体育运动的优势项目，某运动员参加10m跳台的跳水比赛，如其质量为m=60kg，其体形可等效为长度L=1.0m，直径d=0.3m的圆柱体，不计空气阻力，运动员站立在跳台上向上跳起到达最高点时，他的重心离跳台台面的高度为1.3m，在从起跳到接触水面过程中完成一系列动作，入水后水的等效阻力F（未包含浮力）作用于圆柱体的下端面，F的数值随入水深度y变化的函数图象如图所示，该直线与F轴相交于F=2.5mg处，与y轴相交于y=h?（某一未知深度），已知水的密度ρ=1×103㎏/m3，根据以上的数据进行估算（g取10m/s2）．
（1）运动员起跳瞬间所做的功；
（2）运动员起跳瞬间获得的速度大小；
（3）运动员刚接触到水面瞬间的动能；
（4）运动员入水可以达到的最大深度h?（结果保留两位有效数字）．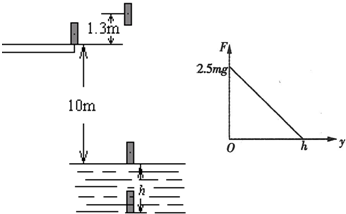

参考答案：（1）运用动能定理研究运动员站立在跳台上向上跳起到达最高点得：
运动员起跳瞬间所做的功为W，
W-mgh1=0-0
W=60×10×（1.3-0.5）=480J
（2）运动员起跳过程
W=12mv2-0?
v=4m/s
（3）运动员从起跳到刚接触水面，运用动能定理得：
mgh′=Ek′-12mv2
解得：运动员刚接触到水面瞬间的动能Ek′=6480J．
（4）运动员从刚接触水面到最深处
mgh-12×2.5mgh-12ρgVL-ρgV（h-L）=0-12mvˊ2
体积V=π（d2）2?L
解得：h=7.98m
答：（1）运动员起跳瞬间所做的功是480J；
（2）运动员起跳瞬间获得的速度大小是4m/s；
（3）运动员刚接触到水面瞬间的动能是6480J；
（4）运动员入水可以达到的最大深度是7.98 m

本题解析：

本题难度：一般

2、简答题  常见的激光器有固体激光器和气体激光器，世界上发达国家已经研究出了自由电子激光器，其原理可简单用图表示：自由电子（设初速度为零）经电场加速后，射入上下排列着许多磁铁的管中，相邻的两块磁铁的极性是相反的，在磁场的作用下电子扭动着前进，犹如小虫在水中游动．电子每扭动一次就会发出一个光子（不计电子发出光子后能量的损失），管子两端的反射镜使光子来回反射，结果从略为透光的一端发射出激光．若加速电压U=1.8×104?V，电子质量为m=0.91×10-30?kg，电子的电量q=1.6×10-19?C，每对磁极间的磁场可看作是均匀的，磁感应强度为B=9×10-4?T，每个磁极的左右宽度为a=30cm，垂直于纸面方向的长度为b=60cm，忽略左右磁极间的缝隙，当电子在磁极的正中间向右垂直于磁场方向射入时，电子可通过几对磁极？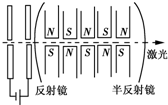

参考答案：

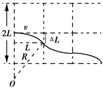
设电子经电场加速获得的速度为v，
由动能定理得，qU=12mv2，
∴v=2qUm=

本题解析：

本题难度：一般

3、选择题  某人用力将一质量为m的物体从离地面高为h的地方竖直上抛，上升的最大高度为H（相对于抛出点），设抛出时初速度为v0，落地时速度为vt，那么此人在抛出物体过程中对物体所做功为（　　）
A．mgH
B．mgh
C．

参考答案：在人推于的过程中，由动能定理可得：
W=12mv02； 故D正确；
对全过程分析可知：
在球运动的过程中，球受人的抛出力做功，重力做功；且已知初动能和末动能，由动能定理可得：
W+mgh=12mvt2-0：
解得人对球所做的功：W=12mvt2-mgh；故C正确；
对于从开始抛到最高点由动能定理可得：
W-mgH=0
故W=mgH，故A正确；
故选ACD．

本题解析：

本题难度：简单

4、计算题  一个质量为m=2kg的铅球从离地面H=2m高处自由落下，落入沙坑中h=5cm深处，如图所示，求沙子对铅球的平均阻力。（g取10m/s2）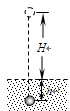

参考答案：f=820N

本题解析：全过程中有重力做功，进入沙中阻力做负功?∴W总=mg（H+h）—fh
由动能定理得：mg（H+h）—fh=0—0
得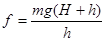?带入数据得f=820N
点评：本题主要是对运动过程的受力分析，正确的选择运动过程，利用动能定理求解

本题难度：简单

5、简答题  证明：质量为m的子弹以水平速度 v1 射入以速度 v2 沿同一方向运动的木块中，木块质量为过程M，当子弹进入木块深度为 d 时，子弹和木块的速度分别为v1′ 和v2′，若木块和子弹的相互作用力恒为f，求这一过程中子弹和木块组成的系统损失的动能。

参考答案：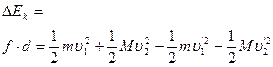

本题解析：设木块位移为 s ，子弹相对木块位移为d，相对地面位移为s + d，根据动能定理：对木块：

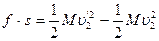
对子弹：

两式相减：

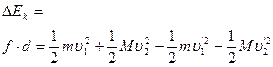
说明：上式表示系统动能损失的数值为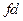，而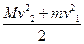为系统在相互作用前的初动能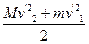，为系统在相互作用后的末初动能，故系统动能的损失等于运动阻力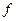与子弹相对木块的位移 d 的乘积，损失的动能转化成系统的内能。此结论可归纳为： 滑动摩擦力和力对应的物体间相对位移的乘积数值上等于系统机械能的损失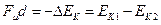，，这结论广泛应用于类似的动能变化关系的问题之中

本题难度：简单